(a) State two factors which can affect the rate of a chemical reaction.
(b) 0.72g of magnesium was added to different volumes of 2 mol. per dm\(^3\) hydrochloric acid. The volume of liberated was as measured at room temperature and pressure. The result of the experiment was as tabulated
| vol. of 2 mol. per dm\(^3\) HCl used (cm\(^3\) | Vol. of H\(_2\) evolved in cm\(^3\) (to the nearest 10cm\(^3\)) |
|
5 15 25 35 45 |
120 360 550 600 600 |
Use the data in the table to plot a graph of the volume of hydrogen liberated against the volume of acid used.
(c) From the graph in (b) above, determine the volume of: (i) hydrogen that would be produced if 50 cm\(^3\) of the acid were added to 0.72g of magnesium.
(ii) the acid which must be added to 0.72 g of magnesium to produce 480 cm\(^3\) of hydrogen;
(iii) the acid needed exactly to dissolve 0.72 g of magnesium completely.
(d) Explain your answer to (c)(iii).
(e) From your answers to (c) above, deduce the: (i) volume of the acid which will dissolve 1 mole of magnesium completely. (Mg = 24)
(ii) volume of hydrogen that would be liberated if 1 mole of magnesium dissolves completely in the acid;
(iii) equation for the reaction between magnesium and hydrochloric acid. Show clearly how you arrived at you answers
Explanation
a) Increase in concentration of reactants increases the rate of reaction. Catalyst increases rate of reaction for an exothermic process.
(b)
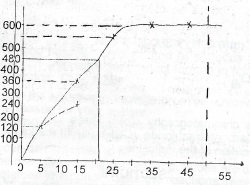
(c)(i) 600cm\(^3\)
(ii) 21 cm\(^3\)
(iii) 35cm\(^3\)
(d) The highest point on the curve above is when the volume of the acid is 35cm\(^3\) and hydrogen gas produces 600cm\(^3\)
(e) (i) 0.72g; Mg to moles \(\frac{0.72}{24}\) = 3 moles
i.e. 3 moles Mg is completely dissoved by 33cm\(^3\)
1 mole Mg will be completly dissolved by \(\frac{35}{3}\) = 11.7
= 11.7 cm\(^3\) Hcl
(ii) 3 moles Mg dissolved to produce 600cm\(^3\) H\(_2\)
1 mole Mg dissolved will produce \(\frac{600}{3}\) = 200 cm\(^3\)
= 200 cm\(^3\)'s vote- . : _me of the acid _00 6 0 —• is 35crr.3 Lind hydrogen :as m-c.- s 600cm3.
H\(_2\)
(iii) Mg\(_{(s)}\) + 2HCl\(_{(aq)}\) + H\(_{2(g)}\)

