(a) Convert the following numbers to be stated bases:
(i) 125.625, to binary
(ii) 111011.10011, to octal
(b) Given that X = 11011011 and Y= 11101101,
(i) construct the truth table for X, Y Z;
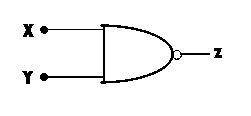
(ii) draw the logic gate of X, Y = Z
(iii) state the value of Z.
Explanation
(a)) 125.625, to binary
| 2 | 125 | R |
| 2 | 62 | 1 |
| 2 | 31 | 0 |
| 2 | 15 | 1 |
| 2 | 7 | 1 |
| 2 | 3 | 1 |
| 2 | 1 | 1 |
| 2 | 0 | 1 |
Therefore, 125= 111110
Hence, 125.625 = 1111101.101,
2nd step: 125 to binary
First method: (0.625) = 625/1000 = 25/40 = 5/8
Hence, 5/8 = (4+1)/ 8 = 4/8 + 1/8 = 1/2 + 1/8
1 X 2\(^{-1}\) + 0 X 2 \(^{-2}\) + 1 x 2\(^{-3}\) = 0.101\(_{2}\)
Therefore, 0.625 = 0.101\(_{2}\),
Second method: 0.625*2 = 1.25 Fraction part 1.23 Carry1
0.25 * 2 =0.5 Fraction part 0.5 Carry 0
0.5 * 2 = 1.00 Fraction part 1.00 Cary 1
0.625 = 0.101\(_{-2}\),
Therefore, (i) 111011.10011, to octal
111\(_2\) = 7\(_8\)
011\(_2\) = 3\(_8\)
100\(_2\) = 4\(_8\)
110\(_2\) = 6\(_8\)
111011.10011\(_2\) = 73.46\(_8\)
bi X = 11011011, Y = 11101101
| X | Y | Z = X.Y |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
bii is shown above.
biii Z = 11001001

