A body is kept at rest by three forces \(F_{1} = (10N, 030°), F_{2} = (10N, 150°)\) and \(F_{3}\). Find \(F_{3}\).
- A. (12N, 090°)
- B. (10N, 270°)
- C. (10N, 180°)
- D. (10N, 120°)
If \(\frac{^{n}C_{3}}{^{n}P_{2}} = 1\), find the value of n.
- A. 8
- B. 7
- C. 6
- D. 5
Find the equation of the straight line that passes through (2, -3) and perpendicular to the line 3x – 2y + 4 = 0.
- A. 2y - 3x = 0
- B. 3y - 2x + 5 = 0
- C. 3y + 2x + 5 = 0
- D. 2y - 3x - 5 = 0
If \(V = \begin{pmatrix} -2 \\ 4 \end{pmatrix}\) and \(U = \begin{pmatrix} -1 \\ 5 \end{pmatrix}\), find \(|U + V|\).
- A. \(3\sqrt{10}\)
- B. \(\sqrt{82}\)
- C. 15
- D. \(2\sqrt{5}\)
Calculate the mean deviation of 1, 2, 3, 4, 5, 5, 6, 7, 8, 9.
- A. 2
- B. 3
- C. 4
- D. 5
If \(g(x) = \frac{x + 1}{x – 2}, x \neq -2\), find \(g^{-1}(2)\).
- A. 3
- B. 2
- C. \(\frac{3}{4}\)
- D. -3
P and Q are the points (3, 1) and (7, 4) respectively. Find the unit vector along PQ.
- A. \(\begin{pmatrix} 4 \\ 3 \end{pmatrix}\)
- B. \(\begin{pmatrix} 0.6 \\ 0.8 \end{pmatrix}\)
- C. \(\begin{pmatrix} 0.8 \\ 0.6 \end{pmatrix}\)
- D. \(\begin{pmatrix} -0.8 \\ 0.6 \end{pmatrix}\)
Two out of ten tickets on sale for a raffle draw are winning tickets. If a guest bought two tickets, what is the probability that both tickets are winning tickets?
- A. \(\frac{1}{80}\)
- B. \(\frac{1}{45}\)
- C. \(\frac{1}{20}\)
- D. \(\frac{1}{10}\)
Given that \(P = \begin{pmatrix} 3 & 4 \\ 2 & x \end{pmatrix}; Q = \begin{pmatrix} 1 & 3 \\ -2 & 4 \end{pmatrix}; R = \begin{pmatrix} -5 & 25 \\ -8 & 26 \end{pmatrix}\) and PQ = R, find the value of x.
- A. -5
- B. -2
- C. 2
- D. 5
Find the upper quartile of the following scores: 41, 29, 17, 2, 12, 33, 45, 18, 43 and 5.
- A. 45
- B. 41
- C. 33
- D. 21
If \(2\sin^{2}\theta = 1 + \cos \theta, 0° \leq \theta \leq 90°\), find \(\theta\).
- A. 30°
- B. 45°
- C. 60°
- D. 90°
If \(s = 3i – j\) and \(t = 2i + 3j\), find \((t – 3s).(t + 3s)\).
- A. -77
- B. -71
- C. -53
- D. -41
A particle is acted upon by two forces 6N and 3N inclined at an angle of 120° to each other. Find the magnitude of the resultant force.
- A. \(18\sqrt{3}\) N
- B. \(27\) N
- C. \(24\) N
- D. \(3\sqrt{3}\) N
The equation of a circle is \(x^{2} + y^{2} – 8x + 9y + 15 = 0\). Find its radius.
- A. 5
- B. \(\frac{1}{2}\sqrt{15}\)
- C. \(\frac{1}{2}\sqrt{85}\)
- D. \(\sqrt{85}\)
Two bodies of masses 3kg and 5kg moving with velocities 2 m/s and V m/s respectively in opposite directions collide. If they move together after collision with velocity 3.5 m/s in the direction of the 5kg mass, find the value of V.
- A. 7.8 m/s
- B. 6.8 m/s
- C. 5.6 m/s
- D. 4.6 m/s
Express \(\frac{x^{2} + x + 4}{(1 – x)(x^{2} + 1)}\) in partial fractions.
- A. \(\frac{x^{2}}{x^{2} + 1} + \frac{x + 4}{1 - x}\)
- B. \(\frac{3}{1 - x} + \frac{2x + 1}{x^{2} + 1}\)
- C. \(\frac{x^{2}}{1 - x} + \frac{x + 4}{x^{2} + 1}\)
- D. \(\frac{3}{1 - x} + \frac{2x + 2}{x^{2} + 1}\)
A circular ink blot on a piece of paper increases its area at the rate \(4mm^{2}/s\). Find the rate of the radius of the blot when the radius is 8mm. \([\pi = \frac{22}{7}]\).
- A. 0.20 mm/s
- B. 0.08 mm/s
- C. 0.25 mm/s
- D. 0.05 mm/s
The sales of five salesgirls on a certain day are as follows; GH¢ 26.00, GH¢ 39.00, GH¢ 33.00, GH¢ 25.00 and GH¢ 37.00. Calculate the standard deviation if the mean sale is GH¢ 32.00.
- A. GH¢ 5.65
- B. GH¢ 5.66
- C. GH¢ 6.5
- D. GH¢ 6.56
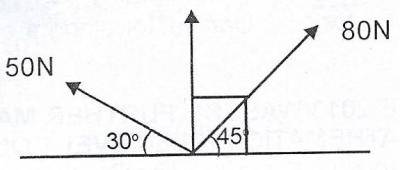
Forces 50N and 80N act on a body as shown in the diagram. Find, correct to the nearest whole number, the horizontal component of the resultant force.
- A. 13N
- B. 43N
- C. 57N
- D. 95N
A committee consists of 5 boys namely: Kofi, John, Ojo, Ozo and James and 3 girls namely: Rose, Ugo and Ama. In how many ways can a sub-committee consisting of 3 boys and 2 girls be chosen, if Ozo must be on the sub-committee?
- A. 35
- B. 30
- C. 18
- D. 12
The function \(f : F \to R\)
= \(f(x) = \begin{cases} 3x + 2 : x > 4 \\ 3x – 2 : x = 4 \\ 5x – 3 : x < 4 \end{cases}\). Find f(4) – f(-3).
- A. 28
- B. 26
- C. -26
- D. -28


