The radius of a sphere is increasing at a rate \(3cm s^{-1}\). Find the rate of increase in the surface area, when the radius is 2cm.
- A. \(8\pi cm^{2}s^{-1}\)
- B. \(16\pi cm^{2}s^{-1}\)
- C. \(24\pi cm^{2}s^{-1}\)
- D. \(48\pi cm^{2}s^{-1}\)
A function is defined by \(h : x \to 2 – \frac{1}{2x – 3}, x \neq \frac{3}{2}\). Find \(h^{-1}(\frac{1}{2})\).
- A. \(6\)
- B. \(\frac{11}{6}\)
- C. \(\frac{11}{4}\)
- D. \(\frac{5}{3}\)
A function is defined by \(h : x \to 2 – \frac{1}{2x – 3}, x \neq \frac{3}{2}\). Find \(h^-1\), the inverse of h.
- A. \(\frac{3x - 4}{2x - 7}, x \neq \frac{7}{2}\)
- B. \(\frac{3x - 7}{2x - 4}, x \neq 2\)
- C. \(\frac{2x - 7}{4x - 3}, x \neq \frac{3}{4}\)
- D. \(\frac{4x - 7}{2x - 4}, x \neq 2\)
If \(T = \begin{pmatrix} -2 & -5 \\ 3 & 8 \end{pmatrix}\), find \(T^{-1}\), the inverse of T.
- A. \(\begin{pmatrix} -8 & -5 \\ 3 & 2 \end{pmatrix}\)
- B. \(\begin{pmatrix} -8 & -5 \\ 3 & -2 \end{pmatrix}\)
- C. \(\begin{pmatrix} -8 & -5 \\ -3 & 2 \end{pmatrix}\)
- D. \(\begin{pmatrix} -8 & -5 \\ -3 & -2 \end{pmatrix}\)
Find the derivative of \(\sqrt[3]{(3x^{3} + 1}\) with respect to x.
- A. \(\frac{3x}{3(3x^{3} + 1)}\)
- B. \(\frac{3x^{2}}{\sqrt[3]{(3x^{3} + 1)^{2}}}\)
- C. \(\frac{3x}{\sqrt[3]{3x^{2} + 1}}\)
- D. \(\frac{3x^{2}}{3(3x^{2} + 1)^{2}}\)
If \(\frac{x + P}{(x – 1)(x – 3)} = \frac{Q}{x – 1} + \frac{2}{x – 3}\), find the value of (P + Q).
- A. -2
- B. -1
- C. 0
- D. 1
A box contains 5 red and k blue balls. A ball is selected at random from the box. If the probability of selecting a blue ball is \(\frac{2}{3}\), find the value of k.
- A. 5
- B. 6
- C. 8
- D. 10
If \(2, (k+1), 8,…\) form an exponential sequence (GP), find the values of k.
- A. -3 and 5
- B. 5 and -5
- C. 3 and -3
- D. -5 and 3
If \((x + 2)\) and \((3x – 1)\) are factors of \(6x^{3} + x^{2} – 19x + 6\), find the third factor.
- A. \(2x - 3\)
- B. \(3x + 1\)
- C. \(x - 2\)
- D. \(3x + 2\)
Using the binomial expansion \((1+x)^{6} = 1 + 6x + 15x^{2} + 20x^{3} + 15x^{4} + 6x^{5} + x^{6}\), find, correct to 3 dp, the value of \((1.98)^{6}\).
- A. 64.245
- B. 61.255
- C. 60.255
- D. 60.245
Simplify \(\frac{1 + \sqrt{8}}{3 – \sqrt{2}}\).
- A. \(7 + \sqrt{2}\)
- B. \(7 + 7\sqrt{2}\)
- C. \(1 - 7\sqrt{2}\)
- D. \(1 + \sqrt{2}\)
If \(8^{x} ÷ (\frac{1}{4})^{y} = 1\) and \(\log_{2}(x – 2y) = 1\), find the value of (x – y).
- A. \(\frac{5}{4}\)
- B. \(\frac{3}{5}\)
- C. \(1\)
- D. \(\frac{2}{3}\)
If \(f(x) = 3x^{3} + 8x^{2} + 6x + k\) and \(f(2) = 1\), find the value of k.
- A. -67
- B. -61
- C. 61
- D. 67
Given that \(x * y = \frac{x + y}{2}, x \circ y = \frac{x^{2}}{y}\) and \((3 * b) \circ 48 = \frac{1}{3}\), find b, where b > 0.
- A. 8
- B. 6
- C. 5
- D. 4
Given that \(3x + 4y + 6 = 0\) and \(4x – by + 3 = 0\) are perpendicular, find the value of b.
- A. 4
- B. 3
- C. \(\frac{1}{3}\)
- D. \(\frac{1}{4}\)
Simplify: \((1 – \sin \theta)(1 + \sin \theta)\).
- A. \(\sin^{2} \theta\)
- B. \(\sec^{2} \theta\)
- C. \(\tan^{2} \theta\)
- D. \(\cos^{2} \theta\)
If \(\frac{1}{5^{-y}} = 25(5^{4-2y})\), find the value of y.
- A. 4
- B. 2
- C. -4
- D. -5

Forces of magnitude 8N and 5N act on a body as shown above. Calculate, correct to 2 dp, the angle that the resultant makes with the horizontal.
- A. 80.76°
- B. 75.00°
- C. 71.99°
- D. 15.00°
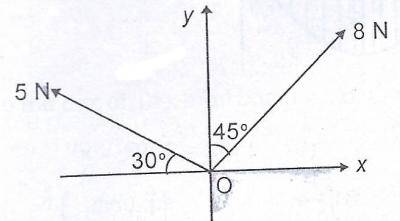
Forces of magnitude 8N and 5N act on a body as shown above. Calculate, correct to 2 d.p., the resultant force acting at O.
- A. 14.06N
- B. 13.00N
- C. 9.83N
- D. 8.26N
Forces \(F_{1} = (8N, 030°)\) and \(F_{2} = (10N, 150°)\) act on a particle. Find the horizontal component of the resultant force.
- A. 1.7N
- B. 4.5N
- C. 9.0N
- D. 13.0N
The sum, \(S_{n}\), of a sequence is given by \(S_{n} = 2n^{2} – 5\). Find the 6th term.
- A. 112
- B. 67
- C. 45
- D. 22


