(a) Find the angle between the vectors \(a = \begin{pmatrix} -3 \\ 4 \end{pmatrix}\) and \(b = \begin{pmatrix} -8 \\ -15 \end{pmatrix}\).
(b) Given that \(a = (4N, 060°)\) and \(b = (3N, 120°)\), find, in component form, the unit vector along \(a – b\).
(a) Given that \(p = (4i – 3j)\) and \(q = (-i + 5j)\), find r such that \(|r| = 15\) and is in the direction \((2p + 3q)\).
(b) 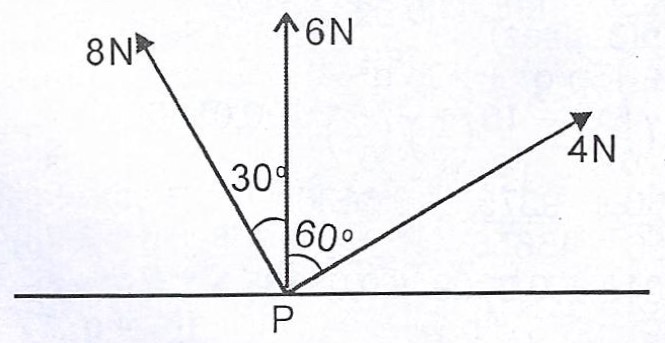
Forces of magnitude 8N, 6N and 4N act at the point P, as shown in the above diagram. Find the : (i) magnitude ; (ii) direction of the resultant force.
(a) A body P of mass 5kg is suspended by two light inextensible strings AP and BP attached to a ceiling. If the strings are inclined at angles 40° and 30° respectively to the downward vertical, find the tension in each of the strings. [Take \(g = 10 ms^{-2}\)].
(b) A constant force F acts on a toy car of mass 5 kg and increases its velocity from 5 ms\(^{-1}\) to 9 ms\(^{-1}\) in 2 seconds. Calculate :
(i) the magnitude of the force ; (ii) velocity of the toy car 3 seconds after attaining a velocity of 9 ms\(^{-1}\).
(a) Two items are selected at random from four items labelled (p, q, r, s).
(i) List the sample space if sampling is done (1) with replacement ; (2) without replacement.
(ii) Find the probability that r is at least one of the two objects selected : (1) in a(i)1 ; (2) in a(i)2.
(b) How many whole numbers from 100 to 999 are divisible by (i) 4 ; (ii) both 3 and 4?
The table gives the distribution of heights in metres of 100 students.
| Height | 1.40-1.42 | 1.43-1.45 | 1.46-1.48 | 1.49-1.51 | 1.52-1.54 | 1.55-1.57 | 1.58-1.60 | 1.61-1.63 |
| Freq | 2 | 4 | 19 | 30 | 24 | 14 | 6 | 1 |
(a) Calculate the : (i) mean height ; (ii) mean deviation of the distribution.
(b) What is the probability that the height of a student selected at random is greater than the mean height of the distribution?
(a) A fair die with six faces is thrown six times. Calculate, correct to three decimal places, the probability of obtaining :
(i) exactly three sixes ; (ii) at most three sixes.
(b) Eight percent of screws produced by a machine are defective. From a random sample of 10 screws produced by the machine, find the probability that :
(i) exactly two will be defective ; (ii) not more than two will be defective.
(a)(i) Find the sum of the series \(A(1 + r) + A(1 + r)^{2} + … + A(1 + r)^{n}\).
(ii) Given that r = 8% and A = GH 40.00, find the sum of the 6th to 10th terms of the series in (i).
(b) Find the equation of the tangent to the curve \(y = \frac{1}{x}\) at the point on the curve when x = 2.
(a) Evaluate : \(\int_{1} ^{4} \frac{x(3x – 2)}{2\sqrt{x}} \mathrm {d} x\)
(b) The equation of a circle is given by \(2x^{2} + 2y^{2} – 8x + 5y – 10 = 0\). Find the :
(i) coordinates of the centre ; (ii) radius of the circle .
(a) Write down the matrix A of the linear transformation \(A(x, y) \to (2x -y, -5x + 3y)\).
(b) If \(B = \begin{pmatrix} 3 & 1 \\ 5 & 2 \end{pmatrix}\), find :
(i) \(A^{2} – B^{2}\) ; (ii) matrix \(C = B^{2} A\) ; (iii) the point \(M(x, y)\) whose image under the linear transformation \(C\) is \(M’ (10, 18)\).
(c) What is the relationship between matrix A and matrix C?
(a) The polynomial \(f(x) = x^{3} + px^{2} – 10x + q\) is exactly divisible by \(x^{2} + x – 6\). Find the :
(i) values of p and q ; (ii) third factor.
(b) The volume of a cube is increasing at the rate of \(2\frac{1}{2} cm^{3} s^{-1}\). Find the rate of change of the side of the base when its length is 2cm.
The marks scored by 35 students in a test are given in the table below.
| Marks | 1-5 | 6-10 | 11-15 | 16-20 | 21-25 | 26-30 |
| Frequency | 2 | 7 | 12 | 8 | 5 | 1 |
Draw a histogram for the distribution.
Simplify \(^{n + 1}C_{4} – ^{n – 1}C_{4}\)
= \(\frac{(n + 1)!}{4! (n – 3)!} – \frac{(n – 1)!}{4! (n – 5)!}\)
= \(\frac{(n + 1)(n)(n – 1)(n – 2)(n – 3)!}{4! (n – 3)!} – \frac{(n – 1)(n – 2)(n – 3)(n – 4)(n – 5)!}{4! (n – 5)!}\)
= \(\frac{(n + 1)(n)(n – 1)(n – 2)}{4!} – \frac{(n – 1)(n – 2)(n – 3)(n – 4)}{4!}\)
= \(\frac{(n – 1)(n – 2) [n(n + 1) – (n – 3)(n – 4)]}{4!}\)
= \(\frac{(n – 1)(n – 2) [n^{2} + n – n^{2} + 7n – 12]}{24}\)
= \(\frac{(n – 1)(n – 2)[8n – 12]}{24}\)
= \(\frac{(n – 1)(n – 2)(2n – 3)}{6}\)
Three forces \(-63j , 32.14i + 38.3j\) and \(14i – 24.25j\) act on a body of mass 5kg. Find, correct to one decimal place, the :
(a) magnitude of the resultant force ;
(b) acceleration of the body.
The gradient function of \(y = ax^{2} + bx + c\) is \(8x + 4\). If the function has a minimum value of 1, find the values of a, b and c.
Write down the first three terms of the binomial expansion \((1 + ax)^{n}\) in ascending powers of x. If the coefficients of x and x\(^{2}\) are 2 and \(\frac{3}{2}\) respectively, find the values of a and n.
The twenty-first term of an Arithmetic Progression is \(5\frac{1}{2}\) and the sum of the first twenty-one terms is \(94\frac{1}{2}\). Find the :
(a) first term ; (b) common difference ; (c) sum of the first thirty terms.
Express \(3x^{2} – 6x + 10\) in the form \(a(x – b)^{2} + c\), where a, b and c are integers. Hence state the minimum value of \(3x^{2} – 6x + 10\) and the value of x for which it occurs.
Two functions g and h are defined on the set R of real numbers by \(g : x \to x^{2} – 2\) and \(h : x \to \frac{1}{x + 2}\). Find :
(a) \(h^{-1}\), the inverse of h ;
(b) \(g \circ h\), when \(x = -\frac{1}{2}\).
Simplify \(\frac{x^{3n + 1}}{x^{2n + \frac{5}{2}}(x^{2n – 3})^{\frac{1}{2}}}\)
- A. \(0\)
- B. \(-\frac{1}{2}\)
- C. \(1\)
- D. \(10\)
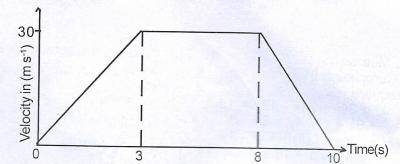
The diagram above is a velocity- time graph of a moving object. Calculate the distance travelled when the acceleration is zero.
- A. 300 m
- B. 90 m
- C. 150 m
- D. 210 m