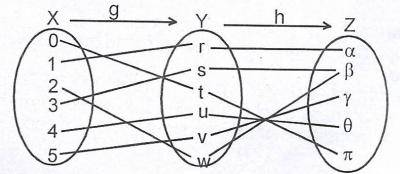
From the diagram above, \(h[g(3)]\) is
- A. s
- B. \(\beta\)
- C. \({s, \beta}\)
- D. \({s, w, \beta}\)
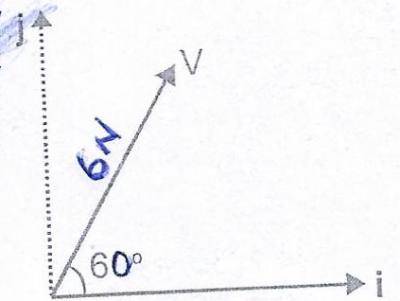
From the diagram above, which of the following represents the vector V in component form?
- A. \(-5\sqrt{3} i + 5j\)
- B. \(3i + 3\sqrt{3}j\)
- C. \(i + 2\sqrt{3}j\)
- D. \(-2\sqrt{3}i - j\)
The angle of a sector of a circle is 0.9 radians. If the radius of the circle is 4cm, find the length of the arc of the sector.
- A. 3.6 cm
- B. 7.6 cm
- C. 8.0 cm
- D. 11.6 cm
The distance s in metres covered by a particle in t seconds is \(s = \frac{3}{2}t^{2} – 3t\). Find its acceleration.
- A. \(1 ms^{-2}\)
- B. \(2 ms^{-2}\)
- C. \(3 ms^{-2}\)
- D. \(4 ms^{-2}\)
A box contains 4 red and 3 blue identical balls. If two are picked at random, one after the other without replacement, find the probability that one is red and the other is blue.
- A. \(\frac{4}{7}\)
- B. \(\frac{2}{7}\)
- C. \(\frac{1}{7}\)
- D. \(\frac{1}{12}\)
Find the acute angle between the lines 2x + y = 4 and -3x + y + 7 = 0.
- A. 40°
- B. 44°
- C. 45°
- D. 54°
Find the number of different arrangements of the word IKOTITINA.
- A. 30240
- B. 60840
- C. 120960
- D. 362880
A straight line makes intercepts of -3 and 2 on the x- and y- axes respectively. Find the equation of the line.
- A. 2x + 3y + 6 = 0
- B. 3x - 2y - 6 = 0
- C. -3x + 2y - 6 = 0
- D. -2x + 3y - 6 =0
Find the constant term in the binomial expansion of \((2x – \frac{3}{x})^{8}\).
- A. 90720
- B. 1296
- C. 1120
- D. 672
Find the values of x at the point of intersection of the curve \(y = x^{2} + 2x – 3\) and the lines \(y + x = 1\).
- A. (1, -2)
- B. (0, 4)
- C. (2, -3)
- D. (1, -4)
If P(x – 3) + Q(x + 1) = 2x + 3, find the value of (P + Q).
- A. 0
- B. 1
- C. 2
- D. 3
A fair die is tossed twice. Find the probability of obtaining a 3 and a 5.
- A. \(\frac{5}{12}\)
- B. \(\frac{2}{3}\)
- C. \(\frac{1}{18}\)
- D. \(\frac{1}{36}\)
Which of the following is nor a measure of central tendency?
- A. Mean
- B. Variance
- C. Median
- D. Mode
Given that \(^{n}P_{r} = 90\) and \(^{n}C_{r} = 15\), find the value of r.
- A. 2
- B. 3
- C. 5
- D. 6
In computing the mean of 8 numbers, a boy mistakenly used 17 instead of 25 as one of the numbers and obtained 20 as the mean. Find the correct mean
- A. 19
- B. 21
- C. 23
- D. 24
Find the unit vector in the direction of the vector \(-12i + 5j\).
- A. \(\frac{-12i}{13} - \frac{5j}{13}\)
- B. \(\frac{-1i}{13} + \frac{5j}{13}\)
- C. \(\frac{-12i}{13} + \frac{5j}{13}\)
- D. \(\frac{-5i}{13} + \frac{12j}{13}\)
Two forces 10N and 6N act in the directions 060° and 330° respectively. Find the x- component of their resultant.
- A. \(5\sqrt{3} - 3\)
- B. \(3 - 5\sqrt{3}\)
- C. \(5 - 3\sqrt{3}\)
- D. \(3\sqrt{3} - 5\)
Differentiate \(\frac{x}{x + 1}\) with respect to x.
- A. \(\frac{1}{x + 1}\)
- B. \(\frac{1}{(x + 1)^{2}}\)
- C. \(\frac{1 - x}{x + 1}\)
- D. \(\frac{1 - x}{(x + 1)^{2}}\)
A stone is dropped from a height of 45m. Find the time it takes to hit the ground. \([g = 10 ms^{-2}]\)
- A. 3.0 seconds
- B. 4.5 seconds
- C. 5.0 seconds
- D. 9.0 seconds
If r denotes the correlation coefficient between two variables, which of the following is always true?
- A. \(0 < r \leq 1\)
- B. \(-1 \leq r < 1\)
- C. \(-1 < r \leq 0\)
- D. \(-1 \leq r \leq 1\)
The marks obtained by 10 students in a test are as follows: 3, 7, 6, 2, 8, 5, 9, 1, 4 and 10. Find the variance.
- A. 8.25
- B. 8.50
- C. 9.00
- D. 9.17


