(a) A body P of mass 5kg is suspended by two light inextensible strings AP and BP attached to a ceiling. If the strings are inclined at angles 40° and 30° respectively to the downward vertical, find the tension in each of the strings. [Take \(g = 10 ms^{-2}\)].
(b) A constant force F acts on a toy car of mass 5 kg and increases its velocity from 5 ms\(^{-1}\) to 9 ms\(^{-1}\) in 2 seconds. Calculate :
(i) the magnitude of the force ; (ii) velocity of the toy car 3 seconds after attaining a velocity of 9 ms\(^{-1}\).
Explanation
(a) 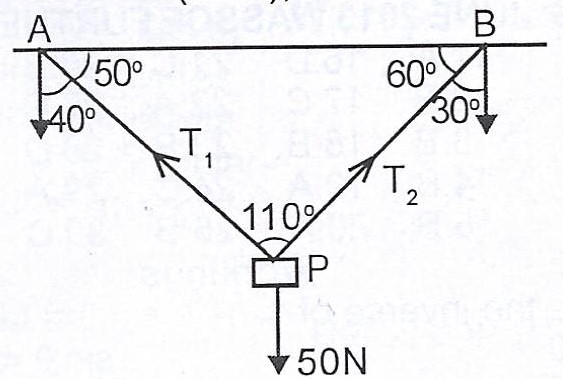
From Lami's theorem,
\(\frac{T_{1}}{\sin 150} = \frac{T_{2}}{\sin 140} = \frac{50}{\sin 70}\)
\(T_{1} = \frac{50 \sin 150}{\sin 70}\)
= \(\frac{50 \times 0.5}{0.9397} = 26.6N\)
\(T_{2} = \frac{50 \sin 140}{\sin 70}\)
= \(\frac{50 \times 0.6428}{0.9397} = 34.2N\)
The tensions are 26.6N and 34.2N respectively.
(b)(i) Given F = ?, u = 5 ms\(^{-1}\) ; v = 9 ms\(^{-1}\) ; t = 2s.
acceleration, \(a = \frac{v - u}{t}\)
= \(\frac{9 - 5}{2} = 2 ms^{-2}\)
Force, \(F = ma = 5 \times 2 \)
= \(10N\).
(ii) \(v = u + at\)
\(u = 9 ms^{-1}; a = 2 ms^{-2} ; t = 2s\)
\(v = 9 + 2(3)\)
= \(9 + 6 = 15 ms^{-1}\).

