A side of a rectangle is three times the other. If the perimeter increases by 2%, find the percentage increase in the area of the rectangle.
Explanation
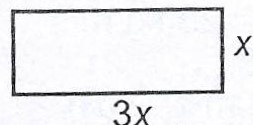
Area, \(A = 3x^{2}\)
Perimeter, \(P = 8x\)
\(\therefore A = \frac{3P^{2}}{64}\)
Let \(P_{1}\) and \(A_{1}\) be the new perimeter and area respectively.
Perimeter increases by 2%
\(\therefore P_{1} = 1.02P\)
\(A_{1} = \frac{3(1.02P)^{2}}{64}\)
\(\frac{A_{1}}{A} = \frac{3(1.02P)^{2}}{64} \times \frac{64}{3P^{2}}\)
= 1.0404
\(A_{1} = 1.0404A = A + 0.0404A\)
Increase in A = 0.0404A.
% increase = \(0.0404 \times 100 = 4.04%\)

