The displacement S metres of a particle from a fixed point O at time t seconds is given by \(S = t^{2} – 6t + 5\).
(a) On a graph sheet, draw a displacement- time graph for the interval \(0 \leq x \leq 6\).
(b) From the graph, find the : (i) time at which the velocity is zero ; (ii) average velocity over the interval \(0 \leq x \leq 4\) ; (iii) total distance covered in the interval \(0 \leq x \leq 5\).
Explanation
(a) \(s = t^{2} - 6t + 5\)
| t (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| s (m) | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
Scale : On time- axis, 2 cm rep 2 s
On displacement, 2 cm rep 2m.
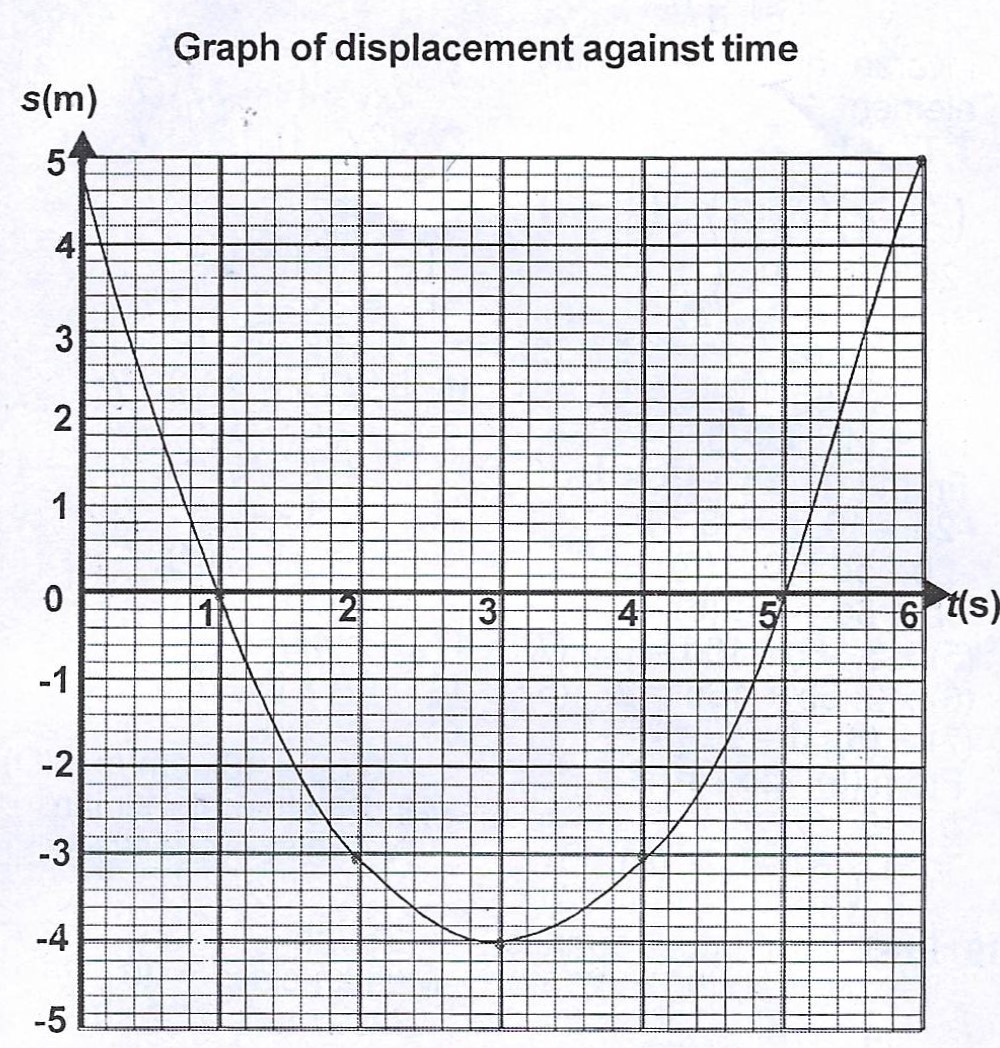
(b)(i) Velocity = \(\frac{\mathrm d s}{\mathrm d t} = Gradient\)
Velocity = 0 m/s when t = 3s
(ii) Average velocity = \(\frac{\text{total costume}}{\text{total time}}\)
\(\frac{5 + 4 + (4 - 3)}{4}\)
= \(\frac{10}{4} = 2.5 m/s\).
(iii) Total distance covered in the interval \(0 \leq x \leq 5\)
= 5 + 4 + 4 = 13m.

