(a) A(-1, 2), B(3, 5) and C(4, 8) are the vertices of triangle ABC. Forces whose magnitudes are 5N and \(3\sqrt{10}\)N act along \(\overrightarrow{AB}\) and \(\overrightarrow{CB}\) respectively. Find the direction of the resultant of the forces.
(b) A particle starts from rest and moves in a straight line. It attains a velocity of 20 m/s after covering a distance of 8 metres. Calculate :
(i) its acceleration ; (ii) the time it will take to cover a distance of 40 metres.
(a) Given that \(x = 3i – j, y = 2i + kj\) and the cosine of the angle between x and y is \(\frac{\sqrt{5}}{5}\), find the values of the constant k.
(b) In the quadrilateral ABCD,
 \(\overrightarrow{AB} = \begin{pmatrix} -5 \\ -1 \end{pmatrix}, \overrightarrow{AC} = \begin{pmatrix} -6 \\ -9 \end{pmatrix}\)
\(\overrightarrow{AB} = \begin{pmatrix} -5 \\ -1 \end{pmatrix}, \overrightarrow{AC} = \begin{pmatrix} -6 \\ -9 \end{pmatrix}\)
and \(\overrightarrow{BD} = \begin{pmatrix} 4 \\ -7 \end{pmatrix}\). Show whether or not ABCD is a parallelogram.
The probabilities that Kofi, Kwasi and Ama will pass a certain examination are \(\frac{9}{10}, \frac{4}{5}\) and x respectively. If the probability that only one of them will pass the examination is \(\frac{9}{50}\), find the :
(a) value of x ;
(b) probability that at least one of them will pass the examination.
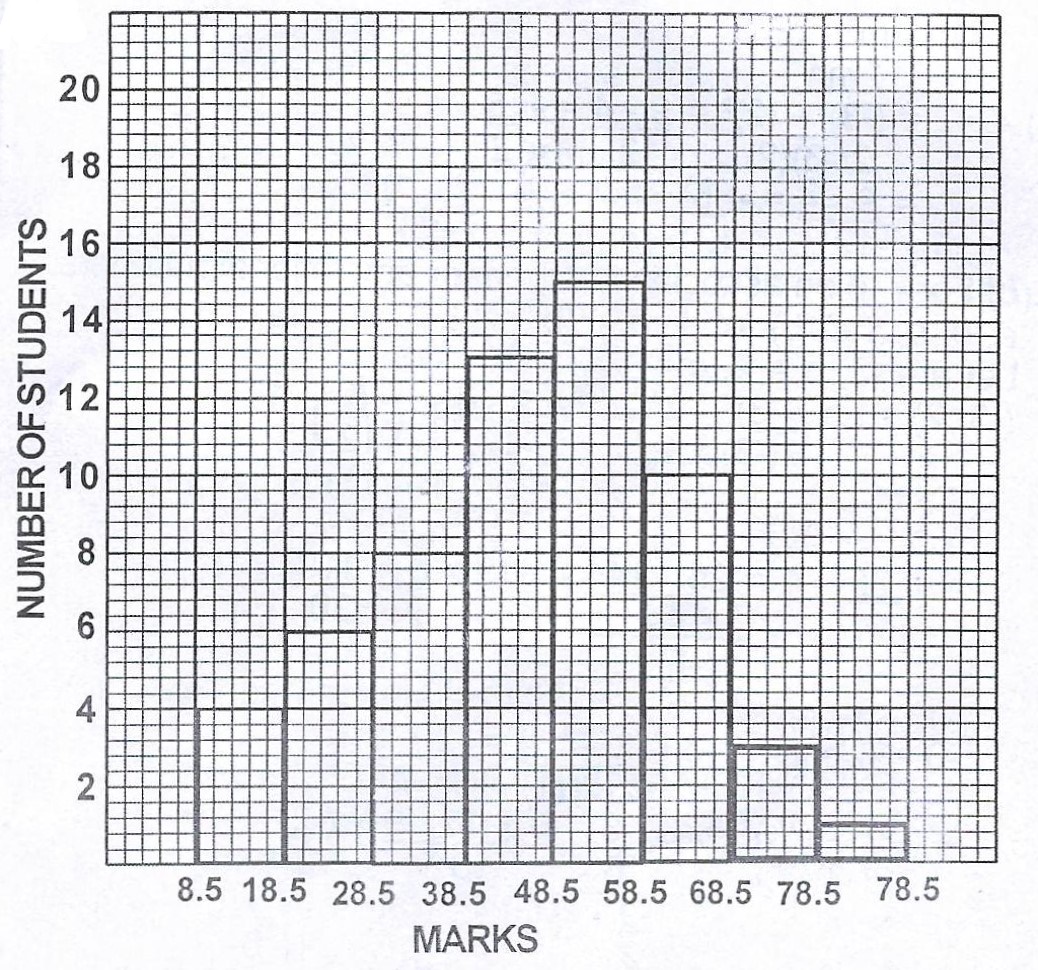
The histogram above represents the scores of some candidates in an examination.
(a) Using the histogram, construct a frequency distribution table indicating clearly the class intervals ;
(b) Draw a cumulative frequency curve of the distribution and use it to estimate the :
(i) median ; (ii) quartile deviation.
(a) If \(f(x) = \frac{x – 3}{2x – 1} , x \neq \frac{1}{2}\) and \(g(x) = \frac{x – 1}{x + 1}, x \neq -1\), fing \(g \circ f\).
(b)(i) Sketch the curve \(y = 9x – x^{3}\) ; (ii) Calculate the total area bounded by the x- axis and the curve \(y = 9x – x^{3}\).
(a) Express \(\frac{5 + \sqrt{2}}{3 – \sqrt{2}} – \frac{5 – \sqrt{2}}{3 + \sqrt{2}}\) in the form \(a + b\sqrt{2}\).
(b) Solve the following equations simultaneously using the determinant method.
\(3x – y – z = -2\)
\(x + 5y + 2z = 5 \)
\(2x + 3y + z = 0\)
(a) Differentiate \((x – 3)(x^{2} + 5)\) with respect to x.
(b) If \((x + 1)^{2}\) is a factor of \(f(x) = x^{3} + ax^{2} + bx + 3\), where a and b are constants, find the :
(i) values of a and b ; (ii) zeros of f(x).
The table shows the distribution of the lengths of 20 iron rods measured in metres :
| Length (m) | 1.0 – 1.1 | 1.2 – 1.3 | 1.4 – 1.5 | 1.6 – 1.7 | 1.8 – 1.9 |
| Frequency | 2 | 3 | 8 | 5 | 2 |
Using an assumed mean of 1.45, calculate the mean of the distribution.
A committee of 3 is formed from a panel of 5 men and 3 women. Find the :
(a) number of ways of forming the committee ;
(b) probability that at least one woman is on the committee.
The position vectors of P, Q and R are \(11i + j, 5i + \frac{13}{3}j\) and \(2i + 6j\) respectively.
(a) Show that P, Q and R lie on a straight line.
(b) Find the ratio of \(|\overrightarrow{PQ}| : |\overrightarrow{QR}|\)
Find the gradient of \(xy^{2} + x^{2} y = 4xy\) at the point (1, 3).
If \(\alpha\) and \(\beta\) are the roots of \(3x^{2} + 5x + 1 = 0\), evaluate \(27(\alpha^{3} + \beta^{3})\).
A binary operation \(\ast\) is defined on the set of rational numbers by \(m \ast n = \frac{m^{2} – n^{2}}{2mn}, m \neq 0 ; n \neq 0\).
(a) Find \(-3 \ast 2\).
(b) Show whether or not \(\ast\) is associative.
Express (14N, 240°) as a column vector.
- A. \(\begin{pmatrix} -7 \\ -7\sqrt{3} \end{pmatrix}\)
- B. \(\begin{pmatrix} 7\sqrt{3} \\ 7\sqrt{3} \end{pmatrix}\)
- C. \(\begin{pmatrix} -7\sqrt{3} \\ -7 \end{pmatrix}\)
- D. \(\begin{pmatrix} 7 \\ -7\sqrt{3} \end{pmatrix}\)
Evaluate \(\frac{\tan 120° + \tan 30°}{\tan 120° – \tan 60°}\)
- A. \(\sqrt{3} + \sqrt{2}\)
- B. \(\frac{2}{3}\)
- C. \(\frac{1}{3}\)
- D. \(-2\sqrt{3}\)
Find \(\lim\limits_{x \to 3} (\frac{x^{3} + x^{2} – 12x}{x^{2} – 9})\)
- A. \(\frac{7}{2}\)
- B. \(0\)
- C. \(\frac{-7}{2}\)
- D. \(-7\)
Find the distance between the points (2, 5) and (5, 9).
- A. 4 units
- B. 5 units
- C. 12 units
- D. 14 units
A ball is thrown vertically upwards with a velocity of 15\(ms^{-1}\). Calculate the maximum height reached. \([g = 10ms^{-2}]\)
- A. 15.25m
- B. 13.25m
- C. 11.25m
- D. 10.25m
If the points (-1, t -1), (t, t – 3) and (t – 6, 3) lie on the same straight line, find the values of t.
- A. t = -2 and 3
- B. t = 2 and -3
- C. t = 2 and 3
- D. t = -2 and -3


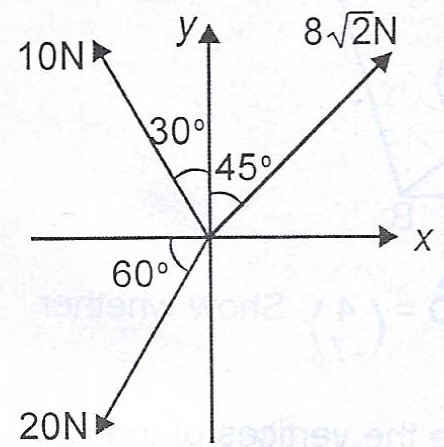 Find the direction of the resultant of the forces in the diagram.
Find the direction of the resultant of the forces in the diagram.