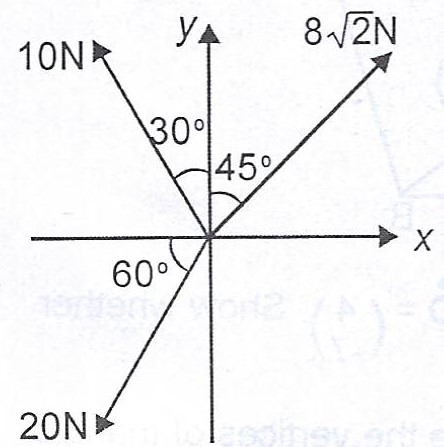
Find the direction of the resultant of the forces in the diagram.
Explanation
\(R_{1} = \begin{pmatrix} -20 \cos 60° \\ -20 \sin 60° \end{pmatrix} ; R_{2} = \begin{pmatrix} -10 \cos 60° \\ 10 \sin 60° \end{pmatrix} \)
\(R_{3} = \begin{pmatrix} 8\sqrt{2} \cos 45° \\ 8\sqrt{2} \sin 45° \end{pmatrix}\)
\(R = R_{1} + R_{2} + R_{3}\)
\(R = \begin{pmatrix} -20 \cos 60° \\ -20 \sin 60° \end{pmatrix} + \begin{pmatrix} -10 \cos 60° \\ 10 \sin 60° \end{pmatrix} + \begin{pmatrix} 8\sqrt{2} \cos 45° \\ 8\sqrt{2} \sin 45° \end{pmatrix}\)
\(R = \begin{pmatrix} -20 \times \frac{1}{2} \\ -20 \times \frac{\sqrt{3}}{2} \end{pmatrix} + \begin{pmatrix} -10 \times \frac{1}{2} \\ 10 \times \frac{\sqrt{3}}{2} \end{pmatrix} + \begin{pmatrix} 8\sqrt{2} \times \frac{1}{\sqrt{2}} \\ 8\sqrt{2} \times \frac{1}{\sqrt{2}} \end{pmatrix}\)
= \(\begin{pmatrix} - 10 - 5 + 8 \\ -10\sqrt{3} + 5\sqrt{3} + 8 \end{pmatrix}\)
= \(\begin{pmatrix} -7 \\ 8 - 5\sqrt{3} \end{pmatrix} = \begin{pmatrix} -7 \\ -0.66 \end{pmatrix}\)
Let \(\theta\) be the direction from the horizontal.
\(\tan \theta = \frac{-0.66}{-7}\)
\(\tan \theta = 0.0943\)
\(\theta = \tan^{-1} (0.0943) = 5.39°\)