(a) Given that \(x = 3i – j, y = 2i + kj\) and the cosine of the angle between x and y is \(\frac{\sqrt{5}}{5}\), find the values of the constant k.
(b) In the quadrilateral ABCD,
\(\overrightarrow{AB} = \begin{pmatrix} -5 \\ -1 \end{pmatrix}, \overrightarrow{AC} = \begin{pmatrix} -6 \\ -9 \end{pmatrix}\)
and \(\overrightarrow{BD} = \begin{pmatrix} 4 \\ -7 \end{pmatrix}\). Show whether or not ABCD is a parallelogram.
Explanation
(a) \(x = 3i - j ; y = 2i + kj\)
\(x \cdot y = |x||y| \cos \theta\)
\((3i - j) \cdot (2i + kj) = (\sqrt{3^{2} + (-1)^{2}})(\sqrt{2^{2} + k^{2}}) \cos \theta\)
\(6 - k = (\sqrt{10})(\sqrt{4 + k^{2}})(\frac{\sqrt{5}}{5})\)
\(5(6 - k) = \sqrt{10(4 + k^{2})(5)}\)
\(30 - 5k = \sqrt{200 + 50k^{2}}\)
\((30 - 5k)^{2} = 200 + 50k^{2}\)
\(900 - 300k + 25k^{2} = 200 + 50k^{2}\)
\(900 - 200 - 300k + 25k^{2} - 50k^{2} = 0\)
\(25k^{2} + 300k - 700 = 0 \implies k^{2} + 12k - 28 = 0\)
\(k^{2} - 2k + 14k - 28 = 0 \implies k(k - 2) + 14(k - 2) = 0\)
\(\text{k = 2 or -14}\).
(b)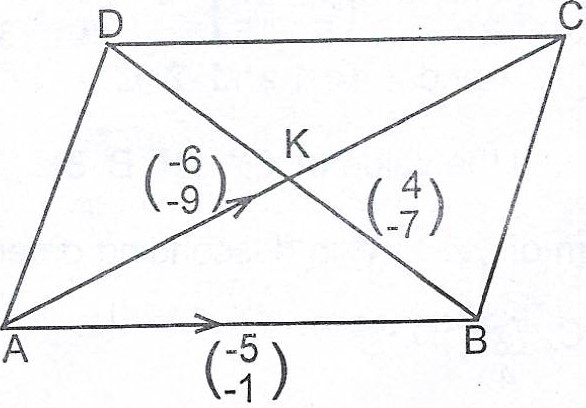 
ABCD is a parallelogram if AD = BC.
\(\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BD}\)
= \(\begin{pmatrix} -5 \\ -1 \end{pmatrix} + \begin{pmatrix} 4 \\ -7 \end{pmatrix}\)
= \(\begin{pmatrix} -1 \\ -8 \end{pmatrix}\)
\(\overrightarrow{BC} = \overrightarrow{BA} + \overrightarrow{AC}\)
= \(\begin{pmatrix} 5 \\ 1 \end{pmatrix} + \begin{pmatrix} -6 \\ -9 \end{pmatrix}\)
= \(\begin{pmatrix} -1 \\ -8 \end{pmatrix}\).
\(\overrightarrow{AD} = \overrightarrow{BC}\). ABCD is a parallelogram.