(a) A(-1, 2), B(3, 5) and C(4, 8) are the vertices of triangle ABC. Forces whose magnitudes are 5N and \(3\sqrt{10}\)N act along \(\overrightarrow{AB}\) and \(\overrightarrow{CB}\) respectively. Find the direction of the resultant of the forces.
(b) A particle starts from rest and moves in a straight line. It attains a velocity of 20 m/s after covering a distance of 8 metres. Calculate :
(i) its acceleration ; (ii) the time it will take to cover a distance of 40 metres.
Explanation
(a) 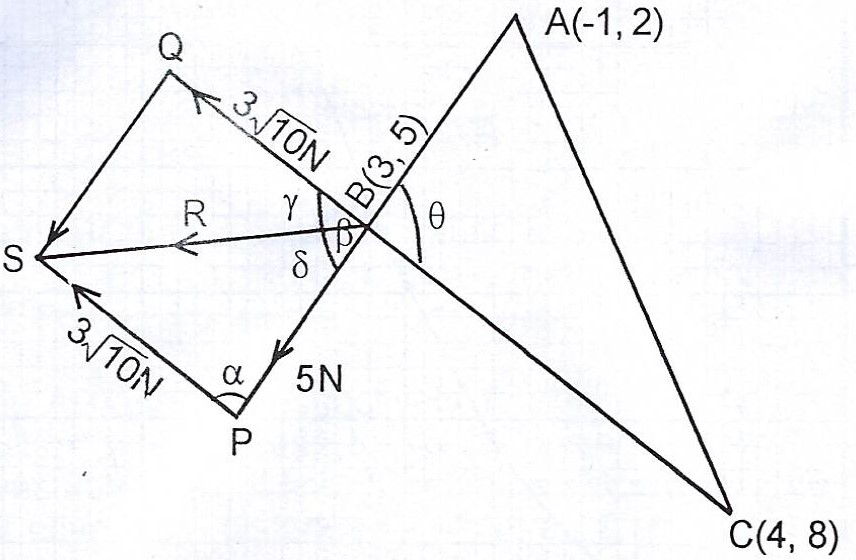
\(|AB| = \sqrt{(-1 - 3)^{2} + (2 - 5)^{2}}\)
= \(\sqrt{16 + 9} = \sqrt{25}\)
= 5 units.
\(|AC| = \sqrt{(4 - 1)^{2} + (8 - 2)^{2}}\)
= \(\sqrt{25 + 36}\)
= \(\sqrt{61}\) units.
\(|BC| = \sqrt{(4 - 3)^{2} + (8 - 5)^{2}}\)
= \(\sqrt{1 + 9} \)
= \(\sqrt{10}\) units.
From the cosine rule,
\((\sqrt{61})^{2} = 5^{2} + (\sqrt{10})^{2} - 2(5)(\sqrt{10}) \cos <PBQ\)
\(\cos < PBQ = \frac{25 + 10 - 61}{2(5)(\sqrt{10})}\)
\(\cos < PBQ = \frac{-26}{10\sqrt{10}} = -0.4747\)
\(< PBQ = 118°, \beta = < PBQ = 118°\)
\(< BPS = \alpha = 180° - 118° = 62°\)
The magnitude of the resultant
\(|R|^{2} = 5^{2} + (3\sqrt{10})^{2} - 2(5)(3\sqrt{10}) \cos 62\)
= \(25 + 90 - (30\sqrt{10})(0.4695)\)
= \(115 - 44.538\)
= \(70.462\)
\(|R| = \sqrt{70.462} = 8.39N\)
Let \(\delta\) be the angle the resultant makes with the 5N force.
\(PS^{2} = BS^{2} + BP^{2} - 2(BS)(BP) \cos PBS\)
\((3\sqrt{10})^{2} = (\sqrt{70.462})^{2} + 5^{2} - 2(8.39)(5) \cos \delta\)
\(90 = 70.462 + 25 - 83.9 \cos \delta\)
\(\cos \delta = \frac{70.462 + 25 - 90}{83.9}\)
\(\cos \delta = 0.0651\)
\(\delta = \cos^{-1} (0.0651) = 86.27°\)
\(\approxeq 86°\).
The resultant makes an angle of 86° with the 5N force.
(b)(i) \(u = 0 ms^{-1} ; v = 20 ms^{-1} ; s = 8 m ; a = ?\)
\(v^{2} = u^{2} + 2as \)
\(20^{2} = 0^{2} + 2(8)a \implies 400 = 16a\)
\( a = 25 ms^{-2}\)
(ii) \(t = ?\)
\(s = ut + \frac{1}{2} at^{2}\)
\(40 = 0 + \frac{1}{2} (25)(t^{2})\)
\(80 = 25t^{2}\)
\(t^{2} = \frac{80}{25} = 3.2\)
\(t = \sqrt{3.2} = 1.79 s\)
It takes 1.79s to cover a distance of 40m.

