Points (2, 1) and (6, 7) are opposite vertices of a square which is inscribed in a circle. Find the :
(a) centre of the circle ; (b) equation of the circle.
Explanation
(a) 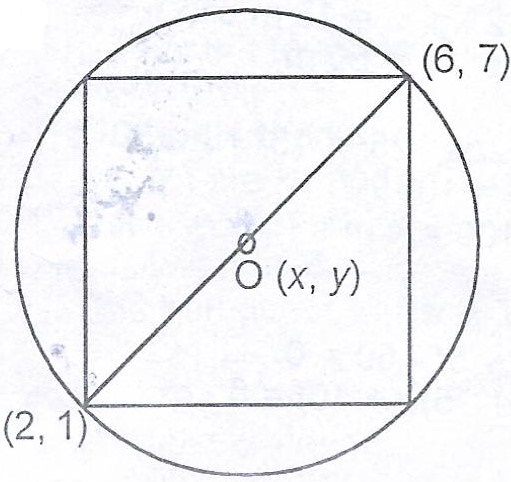
Let O(x, y) be the centre of the circle. O is the midpoint of the two points with given coordinates.
\(x = \frac{2 + 6}{2} = \frac{8}{2} = 4\)
\(y = \frac{1 + 7}{2} = \frac{8}{2} = 4\)
The centre is (4, 4).
(b) Radius of circle = \(\sqrt{(4 - 1)^{2} + (4 - 2)^{2}}\)
= \(\sqrt{3^{2} + 2^{2}}\)
= \(\sqrt{13} units\).
Equation of the circle : \((x - 4)^{2} + (y - 4)^{2} = (\sqrt{13})^{2}\)
\((x^{2} - 8x + 16) + (y^{2} - 8y + 16) = 13\)
\(x^{2} + y^{2} - 8x - 8y + 32 - 13 = 0\)
\(x^{2} + y^{2} - 8x - 8y + 19 = 0\)

