Forces of magnitude 3N, 4N and 2N act along the vectors \(j ; -i + j\) and \(i + j\) respectively. Calculate, correct to one decimal place, the magnitude of the resultant of the forces.
Explanation
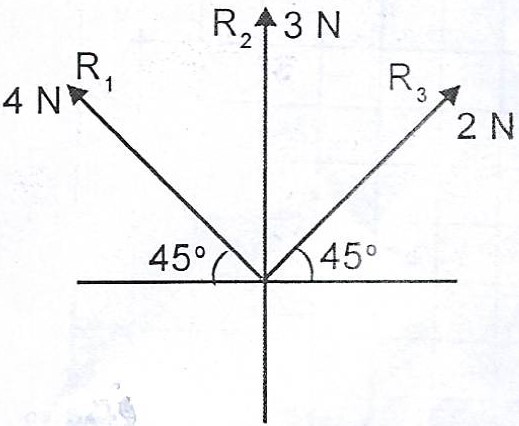
Resultant :
\(R = R_{1} + R_{2} + R_{3}\)
= \(\begin{pmatrix} -4 \cos 45 \\ -4 \sin 45 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \sin 90 \end{pmatrix} + \begin{pmatrix} 2 \cos 45 \\ 2 \sin 45 \end{pmatrix}\)
= \(\begin{pmatrix} -2\sqrt{2} \\ -2\sqrt{2} \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} + \begin{pmatrix} \sqrt{2} \\ \sqrt{2} \end{pmatrix}\)
= \(\begin{pmatrix} - \sqrt{2} \\ 3 - \sqrt{2} \end{pmatrix}\)
\(|R| = \sqrt{(-\sqrt{2})^{2} + (3 - \sqrt{2})^{2}}\)
= \(\sqrt{2 + 11 - 2\sqrt{2}}\)
= \(\sqrt{13 - 2\sqrt{2}}\)
= \(10.1718\)
\(|R| = 3.1893 \approxeq 3.2N\)

