(a) Given that \(\overrightarrow{AB} = \begin{pmatrix} 4 \\ 5 \end{pmatrix}\) and \(\overrightarrow{BC} = \begin{pmatrix} -3 \\ 5 \end{pmatrix}\); find the :
(i) angle between the vectors AB and AC ; (ii) unit vector along \(\overrightarrow{AB} – \overrightarrow{BC}\).
(b) P, Q, R and M are points in the \(O_{XY}\) plane. If \(\overrightarrow{PQ} = 2i + 8j , \overrightarrow{PR} = 11i – 12j\) and M divides QR internally in the ratio 3 : 7, find \(\overrightarrow{PM}\).
Explanation
(a) \(\overrightarrow{AB} = \begin{pmatrix} 4 \\ 5 \end{pmatrix} = 4i + 5j\)
\(\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC}\)
= \(\begin{pmatrix} 4 \\ 5 \end{pmatrix} + \begin{pmatrix} -3 \\ 5 \end{pmatrix}\)
= \(\begin{pmatrix} 1 \\ 10 \end{pmatrix}\)
(i) Let \(\alpha\) be the angle between \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\).
\(\overrightarrow{AB} \cdot \overrightarrow{AC} = |AB||AC| \cos \alpha\)
\((4i + 5j) \cdot (i + 10j) = (\sqrt{4^{2} + 5^{2}})(\sqrt{1^{2} + 10^{2}}) \cos \alpha\)
\(4 + 50 = (\sqrt{41})(\sqrt{101}) \cos \alpha\)
\(\cos \alpha = \frac{54}{(\sqrt{41})(\sqrt{101})}\)
\(\cos \alpha = 0.8392\)
\(\alpha = 32.94°\)
(ii) \(\overrightarrow{AB} - \overrightarrow{BC} = \begin{pmatrix} 4 \\ 5 \end{pmatrix} - \begin{pmatrix} -3 \\ 5 \end{pmatrix}\)
=\(\begin{pmatrix} 7 \\ 0 \end{pmatrix} = 7i\)
\(\overrightarrow{AB} - \overrightarrow{BC} = 7i\)
Unit vector in the direction of 7i = \(\frac{7i}{7} = i\)
(b) \(\overrightarrow{PQ} = \begin{pmatrix} 2 \\ 8 \end{pmatrix} ; \overrightarrow{PR} = \begin{pmatrix} 11 \\ -12 \end{pmatrix}\)
\(\overrightarrow{QR} = \overrightarrow{QP} + \overrightarrow{PR} \)
= \(-\overrightarrow{PQ} + \overrightarrow{PR}\)
= \(\begin{pmatrix} -2 \\ -8 \end{pmatrix} + \begin{pmatrix} 11 \\ -12 \end{pmatrix}\)
= \(\begin{pmatrix} 9 \\ -20 \end{pmatrix}\)
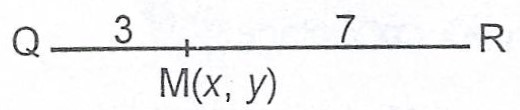
\(\frac{QM}{MR} = \frac{QP + PM}{MP + PR} = \frac{-PQ + PM}{-PM + PR}\)
\(\frac{QM}{MR} = \frac{3}{7}\)
\(7QM = 3MR\)
\(7(-PQ + PM) = 3(-PM + PR)\)
\(7(-PQ) + 7PM = 3(-PM) + 3(PR)\)
\(7(\begin{pmatrix} -2 \\ -8 \end{pmatrix} - 3(\begin{pmatrix} 11 \\ -12 \end{pmatrix} = -10(PM)\)
\(\begin{pmatrix} -47 \\ -20 \end{pmatrix} = -10(PM)\)
\(PM = \begin{pmatrix} 4.7 \\ 2 \end{pmatrix}\)

