(a) Given that \(m = (6i + 8j)\) and \(n = (-8i + \frac{7}{3}j)\), find the :
(i) magnitudes and direction of m and n ; (ii) angle between m and n.
(b) The position vectors of points P, Q, R and S are \(\begin{pmatrix} -2 \\ 3 \end{pmatrix}, \begin{pmatrix} 10 \\ 4 \end{pmatrix}, \begin{pmatrix} 3 \\ 12 \end{pmatrix}\) and \(\begin{pmatrix} 4 \\ 0 \end{pmatrix}\) respectively. Show that \(\overrightarrow{PQ}\) is perpendicular to \(\overrightarrow{RS}\).
Explanation
(a) \(m = (6i + 8j) ; n = (-8i + \frac{7}{3}j)\)
(i) \(|m| = \sqrt{6^{2} + 8^{2}} = \sqrt{36 + 64}\)
= 10 units.
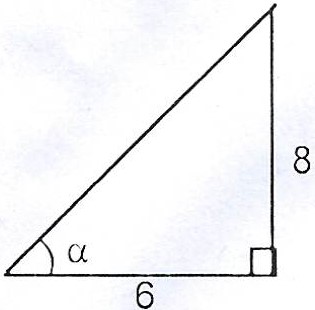
Direction of m: \(\tan \alpha = \frac{8}{6} = 1.333\)
\(\alpha = 53.13°\)
\(|n| = \sqrt{(-8)^{2} + (\frac{7}{3})^{2}} = \sqrt{64 + \frac{49}{9}}\)
= \(\sqrt{\frac{625}{9}} = \frac{25}{3} units\)
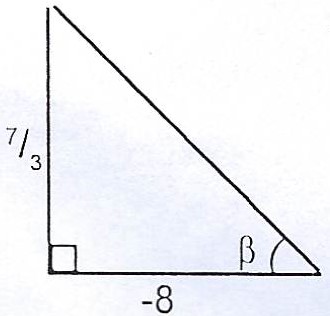
Direction of n :
\(\tan \beta = \frac{\frac{7}{3}}{-8}\)
= \(-\frac{7}{24} = -0.2917\)
\(\beta = \tan^{-1} (-0.2917) = -16.26°\)
(ii) Let the angle between m and n be \(\theta\).
\(m \cdot n = |m||n| \cos \theta\)
\(\cos \theta = \frac{m \cdot n}{|m||n|}\)
\(m \cdot n = (6i + 8j) \cdot (-8i + \frac{7}{3}j)\)
= \(-48 + \frac{56}{3}\)
= \(\frac{-88}{3}\)
\(\cos \theta = \frac{-\frac{88}{3}}{10 \times \frac{25}{3}}\)
= \(\frac{-88}{250}\)
\(\cos \theta = -0.352\)
\(\theta = \cos^{-1} (-0.352) = 110.61°\)
(b) For PQ to be perpendicular to RS, the angle between them should be 90°. That is, \(\cos \theta = 0\).
\(\overrightarrow{PQ} = \begin{pmatrix} 10 \\ 4 \end{pmatrix} - \begin{pmatrix} -2 \\ 3 \end{pmatrix} = \begin{pmatrix} 12 \\ 1 \end{pmatrix}\)
\(\overrightarrow{RS} = \begin{pmatrix} 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 3 \\ 12 \end{pmatrix} = \begin{pmatrix} 1 \\ -12 \end{pmatrix}\)
\(|PQ| = \sqrt{12^{2} + 1^{2}} = \sqrt{144 + 1} = \sqrt{145}\)
\(|RS| = \sqrt{1^{2} + (-12)^{2}} = \sqrt{1 + 144} = \sqrt{145}\)
\(\overrightarrow{PQ} \cdot \overrightarrow{RS} = (12i + j) \cdot (i - 12j)\)
= \(0\)
\(\overrightarrow{PQ} \cdot \overrightarrow{RS} = |PQ||RS| \cos \theta\)
\(\cos \theta = \frac{0}{(\sqrt{145})(\sqrt{145})} = 0\)

