The position vectors of points A, B and C with respect to the origin are (8i – 2j), (2i + 6j) and (-10i + 4j) respectively. If ABCN is a parallelogram, find :
(a) the position vector of N;
(b) AN and AB ;
(c) correct to two decimal place, the acute angle between AN and AB.
Explanation
(a) 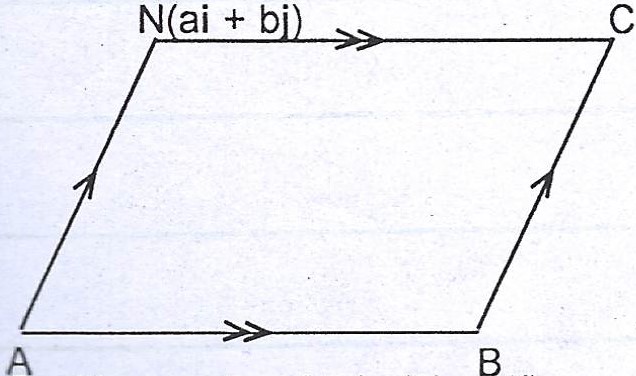
Position vector of A is (8i - 10j)
Position vector of B is (2i + 6j)
Position vector of C is (-10i + 4j).
Let position vector of N be (ai + bj).
ABCN is a parallelogram.
\(\therefore \overrightarrow{AB} = \overrightarrow{NC}\).
\(\begin{bmatrix} (2 - 8)i \\ (6 + 10)j \end{bmatrix} = \begin{bmatrix} (-10 - a)i \\ (4 - b)j \end{bmatrix}\)
Equating components,
\(2 - 8 = -10 - a \implies a = -4\)
\(6 + 10 = 4 - b \implies b = -12\)
The position vector of N is (-4i - 12j).
(b) \(\overrightarrow{AN} \cdot \overrightarrow{AB}\)
\(\overrightarrow{AN} = \bar{A} - \bar{N} \)
= \((8i - 10j) - (-4i - 12j)\)
= \(12i + 2j\)
\(\overrightarrow{AB} = \bar{A} - \bar{B}\)
= \((8i - 10j) - (2i + 6j)\)
= \(6i - 16j\)
\(\therefore \overrightarrow{AN} \cdot \overrightarrow{AB} = (12i + 2j) \cdot (6i - 16j)\)
= \(72 - 32 = 40\)
(c) Let \(\theta\) be the acute angle between \(\overrightarrow{AN}\) and \(\overrightarrow{AB}\).
\(\overrightarrow{AN} \cdot \overrightarrow{AB} = |AN||AB| \cos \theta\)
\(|AN| = |12i + 2j| = \sqrt{12^{2} + 2^{2}} = \sqrt{144 + 4} = \sqrt{148}\)
\(|AB| = |6i - 16j| = \sqrt{6^{2} + (-16)^{2}} = \sqrt{36 + 256} = \sqrt{292}\)
\(\therefore 40 = (\sqrt{148})(\sqrt{292}) \cos \theta\)
\(\cos \theta = \frac{40}{(\sqrt{148})(\sqrt{292})}\)
\(\cos \theta = \frac{40}{207.88} = 0.1924\)
\(\theta = \cos^{-1} (0.1924) = 78.907°\)
\(\approxeq 78.9°\)

