A uniform beam, XY, 4m long and weighing 350N rests on two pivots P and Q. It is kept in equilibrium by weights of 80N attached at X and 1000N attached at a point between P and Q such that it is 0.6m from Q. If XP = 0.8m and PQ = 2.2m.
(a) calculate the reactions at P and Q ;
(b) if the 1000N weight is replaced with a 1200N weight, at what point from Q should it be placed in order to maintain the equilibrium.
Explanation
(a) 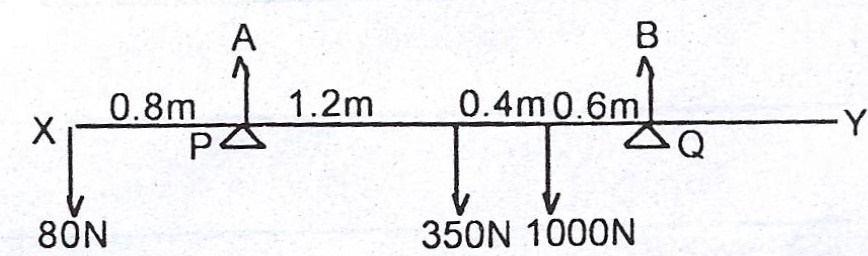
Let A and B be the reactions at P and Q respectively.
A + B = 80 + 350 + 1000 = 1430N
We take moments about Q.
Clockwise moments = 2.2A
Anticlockwise moments = \(80 \times 3 + 350 \times 1 + 1000 \times 0.6\)
= \(1190N\)
Both moments are equal
\(\therefore 2.2A = 1190 \implies A = \frac{1190}{2.2} = 540.9N\)
\(B = 1190N - 540.9N = 649.1N\)
The reactions at P and Q are 540.9N and 649.1N respectively.
(b) 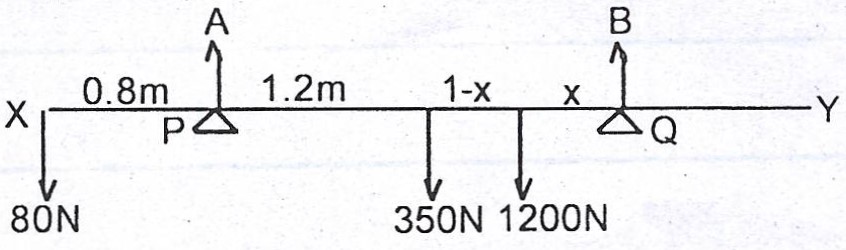
Reaction at P : \((80 + 350 + 1000)N = 540.9N\)
\(\therefore \text{The new reaction at P} = (80 + 350 + 1200)N = \frac{1630}{1430} \times 540.9\)
= \(616.6N\)
Take moments at Q :
\(2.2 \times 616.6 = 80 \times 3 + 350 \times 1 + 1200x\)
\(1200x = 1356.5 - 590\)
\(1200x = 766.5\)
\(x = \frac{766.5}{1200}\)
= \(0.63875 \approxeq 0.64m\)
The 1200N should be placed 0.64m from Q.

