P is the mid-point of \(\overline{NO}\) and equidistant from \(\overline{MN}\) and \(\overline{MO}\) . If \(\overline{MN}\) = 8i + 3j and \(\overline{MO}\) = 14i – 5j, find \(\overline{MP}\) .
Explanation
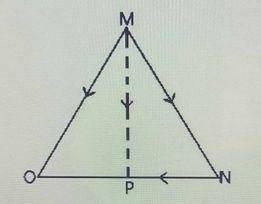
\(\overline{MN}\) = 8i + 3j
\(\overline{MO}\) = 14i - 5j
Consider ∆MON
\(\overline{MN}\) + \(\overline{NO}\) = \(\overline{MO}\)
\(\overline{NO}\) = \(\overline{MO}\) - \(\overline{MN}\)
\(\overline{NO}\) = 14i - 5j - (8i + 3j) = 6i - 8j
Since P is the midpoint of \(\overline{NO}\), then
\(\overline{NP} =\frac{1}{2}( \overline{NO} )\)
\(=\frac{1}{2}(6i - 8j) = 3i - 4j\)
Consider ∆MNP
\(\overline{MN}\) + \(\overline{NP}\) = \(\overline{MP}\)
(8i + 3j) + (3i - 4j) = \(\overline{MP}\)
\(\overline{MP}\) = 8i + 3i + 3j - 4j
∴ \(\overline{MP}\) = 11i - j

