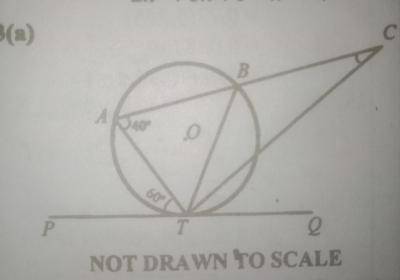
(a) In the diagram above, ABT is a circle centre O. \(\overline{PQ}\) is a tangent to the circle at T and ABC is a straight line. \(\overline{TC}\) bisects \(\angle\)BTQ, \(\angle\)BAT = 44º and \(\angle\)PTA = 60º. Find \(\angle\)ACT
(b) The circumference of the base of a cylindrical tank is 11 m. The height of the tank is 3 m more than 6 times the base radius. Calculate the:
(i) radius; (ii) height; (iii) volume of the tank.
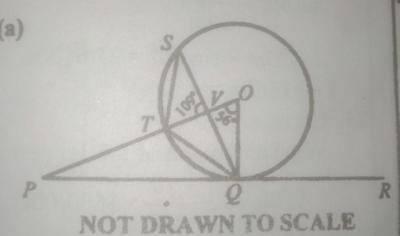
(a) In the diagram above, \(\overline{PR}\) is a tangent to the circle O at Q. \(\angle\)POQ = 56º and \(\overline{PO}\) intersect \(\overline{SO}\) at V such that \(\angle\)SVP = 109º. Calculate: (i) \(\angle\)TQP (ii) \(\angle\)QTS
(b) Simplify \(\frac{2n^2 – 3n – 2 }{2n^2 + 3n + 1} \times \frac{n^2 – 1}{n^2 – 4}\)
(a) Find the equation of the line that passes through the origin and the point of intersection of the lines \( x + 2y = 7 \) and \( x – y = 4 \). (b) The ratio of an interior angle to an exterior angle of a regular polygon is 4: 1. Find the: (i) number of sides; (ii) value of the exterior angle; and (iii) sum of the interior angles of the polygon.
(a) In a man’s will, he gave \(\frac{2}{5}\) of the total acres of the farm to the wife and \(\frac{1}{3}\) of what is left to the family. The rest of the farm was to be shared amongst his three children in the ratio 3: 5: 2. Given that, the child who had the least share received 8 acres, calculate the:
(i) total acres the man left.
(ii) number of acres the wife received.
(b) The price of a Television set is $1,600.00. It can be purchased by a deposit of $400.00 and the rest of the amount paid by 12 monthly installments at 25% per annum simple interest. If the Television set is purchased by installment, find the total cost.
The diameter of a circle centre O is 26 cm. If a chord \(\overline{PQ}\) is drawn such that it is 5 cm from O to the centre of the chord, calculate, correct to the nearest whole number, the
(a)\(\angle\)POQ
(b) Area of the minor segment formed by the chord \(\overline{PQ}\). [take \(\pi\) = \(\frac{22}{7}\)]
Two observers Abu and Badu, 46 m apart, observe a bird on a vertical pole from the same side of the bird. The angles of elevation of the bird from Abu’s and Badu’s eye are 40º and 48º respectively. If at the foot of the pole Abu and Badu are on same horizontal;
(a) illustrate the information in a diagram;
(b) calculate, correct to one decimal place, the height of the pole.
| AGE | 5 | 6 | 7 | 8 | 9 | 10 |
| FREQUENCY | 2 | 2x – 1 | y + 2 | 4 | 2 | y – 1 |
The table shows the ages of 20 children in a household.
Given that x: y = 1: 2
(a) values of x and y
(b) mean ages of the children.
SECTION B
Given that (x + 2), (4x + 3), and (7x + 24) are consecutive terms of a Geometric Progression (G.P.), find the:
a) value of x
b) common ratio.
A basket contains 3 gold-plated marbles, 4 diamond marbles, and some silver marbles, all of the same size and shape. Two marbles were drawn from the basket at random one after the other without replacement. If the probability that the two marbles were all silver is \(\frac{1}{15}\), find the number of silver marbles.
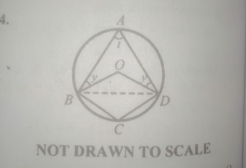
In the diagram, ABCD is a circle O. The quadratic OBCD is a rhombus such that \(\angle\)ADO = \(\angle\)OBA = y and \(\angle\)BAD = t. Find;
(a) the value of t;
(b) the value of y;
(c) \(\angle\)ADC.
A circular floor of a building is to be tiled with ceramic tiles each of side 40 cm. If the perimeter of the floor is 66 m, calculate, correct to the nearest whole number, the number of tiles required to completely tile the floor.[take \(\pi\) = \(\frac{22}{7}\)]
A car travelled at a distance of (2x + 13) km at 67.5 km/h and (5x − 20) km at 72 km/h. If the total time for the entire journey was 90 minutes, find the value of x.
The time(t) taken to buy fuel at a filling station varies directly as the number of vehicles(V) in a queue and varies inversely as the number of pumps (P), available at the station. In a station with 5 pumps, it took 10 minutes to fuel 20 vehicles. find the;
(a) relationship between t, P, and V;
(b) time it takes to fuel 50 vehicles at a station with 2 pumps;
(c) number of pumps required to fuel 40 vehicles in 20 minutes.
For what values of y is \(\frac{y + 2}{8y^2 – 10y + 3}\) not defined?
- A. \(\frac{-3}{4}\), \(\frac{1}{2}\)
- B. \(\frac{-3}{4}\), \(\frac{-1}{2}\)
- C. \(\frac{3}{4}\), \(\frac{1}{2}\)
- D. \(\frac{3}{4}\), \(\frac{-1}{2}\)
The fourth and eighth terms of an Arithmetic Progression are 16 and 40 respectively. Find the common difference.
- A. - 6
- B. 6
- C. -2
- D. 2
Find the range of the following set of numbers: 28, 29, 39, 38, 33, 37, 26, 20, 15, and 25.
- A. 22
- B. 24
- C. 25
- D. 27
Which of the following points lies on the line 3x – 8y = 11?
- A. (1, 1)
- B. (1, -1)
- C. (-1, 1)
- D. (-1, -1)
The probability that Amaka will pass an examination is \(\frac{3}{7}\) and that Bala will pass is \(\frac{4}{9}\). Find the probability that both will pass the examination.
- A. \(\frac{2}{21}\)
- B. \(\frac{4}{21}\).
- C. \(\frac{5}{21}\)
- D. \(\frac{9}{21}\)
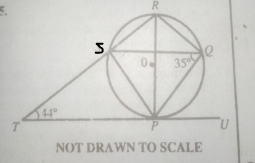
In the diagram \(\overline{TU}\) is a tangent to the circle SPQR at P. If \(\angle\)PTS = 44º, \(\angle\)SQP = 35º, find \(\angle\)PST
- A. 101º
- B. 125º
- C. 130º
- D. 135º
A cliff on the bank of a river 87 m high. A boat on the river is 22 m away from the cliff. Calculate, correct to the nearest degree, the angle of depression of the boat from the top of the cliff.
- A. 76\(^o\)
- B. 64\(^o\)
- C. 36\(^o\)
- D. 24\(^o\)
The area of a sector of a circle with radius 7cm is 51.3 cm\(^2\). Calculate, correct to the nearest whole number, the angle of the sector. (Take \(\pi\) = \(\frac{22}{7}\))
- A. 60\(^0\)
- B. 120\(^0\)
- C. 150\(^0\)
- D. 150\(^0\)


