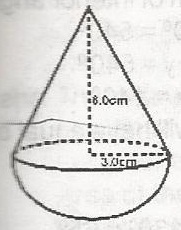
In the figure, a solid consists of a hemisphere surmounted by a right circular cone, with radius 3.0cm and height 6.0cm. Find the volume of the solid
- A. 36\(\pi\)cm 3
- B. 54\(\pi\)cm 2
- C. 18\(\pi\)cm 2
- D. 108\(\pi\)cm 2
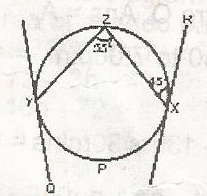
In the figure, XR and YQ are tangents to the circle YZXP if ZXR = 45° and YZX = 55°, Find ZYQ
- A. 135O
- B. 125O
- C. 100O
- D. 90O
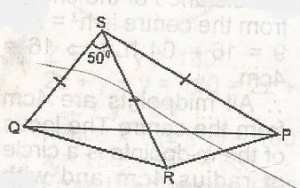
In the figure, PS = RS = QS and QRS = 50°. Find QPR
- A. 25O
- B. 40O
- C. 50O
- D. 65O
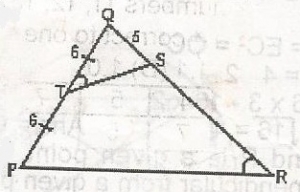
In the figure, STQ = SRP, PT = TQ = 6cm and QS = 5cm. Find SR
- A. \(\frac{47}{5}\)
- B. 5
- C. \(\frac{32}{5}\)
- D. \(\frac{22}{5}\)
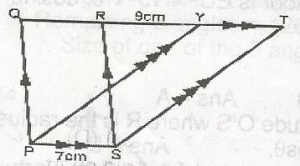
In the figure, PS = 7cm and RY = 9cm. IF the area of parallelogram PQRS is 56cm2. Find the area of trapezium PQTS
- A. 56cm2
- B. 112cm2
- C. 120cm2
- D. 176cm2
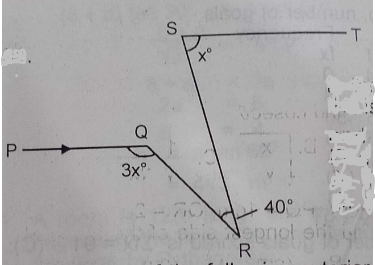
In the figure, PQ is a parallel to ST and QRS = 40o. Find the value of x
- A. 55o
- B. 60o
- C. 65o
- D. 75o
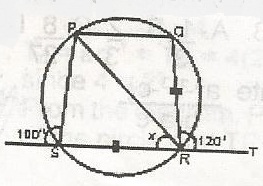
In the figure, PQRS is a circle. If chords QR and RS are equal, calculate the value of x
- A. 80o
- B. 60o
- C. 45o
- D. 40o
If two dice are thrown together, what is the probability of obtaining at least a score of 10?
- A. \(\frac{1}{6}\)
- B. \(\frac{1}{12}\)
- C. \(\frac{5}{6}\)
- D. \(\frac{11}{12}\)
If x and y represent the mean and the median respectively of the following set of numbers 11, 12, 13, 14, 15, 16, 17, 18, 19, 21, find the \(\frac{x}{y}\) correct to one decimal place
- A. 18
- B. 15
- C. 1.0
- D. 5
PQR is a triangle in which PQ = 10cm and QPR = 60oS is a point equidistant from P and Q. Also S is a point equidistant from PQ and PR. If U is the foot of the perpendicular from S on PR, find the length SU in cm to one decimal place
- A. 2.7
- B. 4.33
- C. 3.1
- D. 3.3
If a metal pipe 10cm long has an external diameter of 12cm and a thickness of 1cm find the volume of the metal used in making the pipe
- A. 120\(\pi\)cm3
- B. 110\(\pi\)cm3
- C. 60\(\pi\)cm3
- D. 50\(\pi\)cm3
If \(\cos^2 \theta + \frac{1}{8} = \sin^2 \theta\), find \(\tan \theta\).
- A. 3
- B. \(\frac{3\sqrt{7}}{7}\)
- C. 3\(\sqrt{7}\)
- D. \(\sqrt{7}\)
In triangle PQR, PQ = 1cm, QR = 2cm and PQR = 120o Find the longest side of the triangle
- A. \(\sqrt{3}\)cm
- B. \(\sqrt{7}\)cm
- C. 3cm
- D. 7cm
If cot \(\theta\) = \(\frac{x}{y}\), find cosec\(\theta\)
- A. \(\frac{1}{y}\)(x2 + y2)
- B. \(\frac{x}{y}\)
- C. \(\frac{1}{y}\)\(\sqrt{x^2 + y^2}\)
- D. \(\frac{x - y}{y}\)
Simplify \(\frac{4a^2 – 49b^2}{2a^2 – 5ab – 7b^2}\)
- A. \(\frac{a - b}{2a + b}\)
- B. \(\frac{2a + 7b}{a - b}\)
- C. \(\frac{2a - 7b}{a + b}\)
- D. \(\frac{2a + 7b}{a + b}\)
Simplify \(\frac{1}{x^2 + 5x + 6}\) + \(\frac{1}{x^2 + 3x + 2}\)
- A. \(\frac{x}{(x +2)(x - 3)}\)
- B. \(\frac{2}{(x + 5)(x - 3)}\)
- C. \(\frac{2}{(x + 1)(x + 3)}\)
- D. \(\frac{2}{(x - 1)(x - 3)}\)
The solution of the quadratic equation px2 + qx + b = 0 is
- A. \(\sqrt{\frac{-b \pm b^2 - 4ac}{2a}}\)
- B. \(\frac{-b \pm \sqrt{ p^2 - 4pb}}{2a}\)
- C. \(\frac{-q \pm \sqrt{ q^2 - 4bp}}{2p}\)
- D. \(\frac{-q \pm \sqrt{ p^2 - 4bp}}{2p}\)
Given that 3x – 5y – 3 = 0, 2y – 6x + 5 = 0 the value of (x, y) is
- A. (\(\frac{-1}{8}, \frac{19}{24}\))
- B. 8, \(\frac{24}{19}\)
- C. -8, \(\frac{24}{19}\)
- D. (\(\frac{19}{24}, \frac{-1}{8}\))
List the integral values of x which satisfy the inequality -1 < 5 – 2x \(\geq\) 7
- A. -1, 0, 1, 2
- B. 0, 1, 2, 3
- C. -0, 1, 2, 3
- D. -1, 0, 2, 3
Solve the following equation equation for \(x^2 + \frac{2x}{r^2} + \frac{1}{r^4}\) = 0
- A. r2
- B. \(\frac{1}{r^4}\)
- C. -\(\frac{1}{r^2}\)
- D. 1 - r
Simplify \(\frac{x + 2}{x + 1}\) – \(\frac{x – 2}{x + 2}\)
- A. \(\frac{3}{x + 1}\)
- B. \(\frac{3x + 2}{(x + 1)(x + 2)}\)
- C. \(\frac{5x + 6}{(x + 1)(x + 2)}\)
- D. \(\frac{2x^2 + 5x + 2}{(x + 1)(x + 2)}\)


