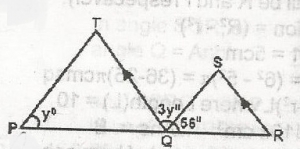
If PQR is a straight line with QS = QR, calculate TPQ, If QT\\SR and TQS = 3yo
- 62o
- 56\(\frac{3}{2}\)o
-
20\(\frac{3}{2}\)o
- 18o
The correct answer is: C
Explanation
Since QS = QRthen, angle SQR = angle SRQ
2 SQR = 180 - 56, SQR = \(\frac{124}{2}\) = 62o
QTP = 62o
QTP = 62o, corresponding angle
3y + 56 + 62 = 180 = 3y = 180 - 118
3y = 62 = 180
3y = 180 - 118
3y = 62
y = \(\frac{62}{3}\)
= 20\(\frac{3}{2}\)