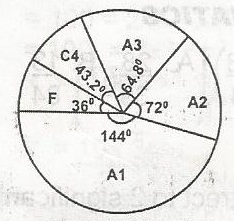
The grades A1, A2, A3, C4 and F earned by students in a particular course are shown in the pie chart. What percentage of the students obtained a C4 grade?
- A. 52.0
- B. 43.2
- C. 40.0
- D. 12.0
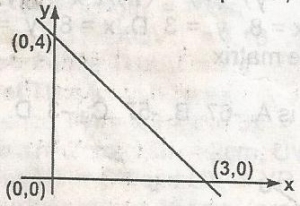
The equation of the line in the graph is
- A. 3y = 4x + 12
- B. 3y = 3x + 12
- C. 3y = -4x + 12
- D. 3y = -4x + 9
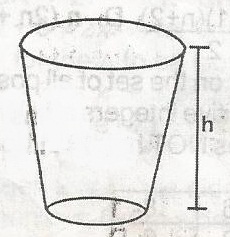
In the frustum of the cone, the top diagram is twice the bottom diameter. If the height of the frustum is h centimeters, find he height of the cone
- A. 2h
- B. 2\(\pi\)h
- C. \(\pi\)h
- D. \(\frac{\pi h}{2}\)
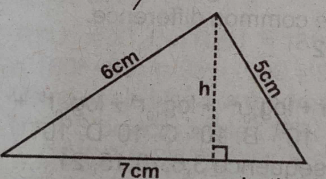
In the diagram. Find h
- A. \(\frac{12}{7}\)cm
- B. \(\frac{12}{7} \sqrt{6}\)cm
- C. \(\frac{7}{12}\)cm
- D. \(\frac{1}{2}\)cm
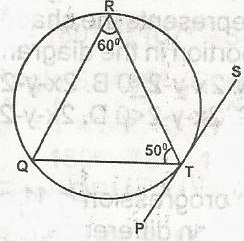
In the diagram, PTS is a tangent to the circle TQR at T. Calculate < RTS
- A. 120o
- B. 70o
- C. 60o
- D. 40o
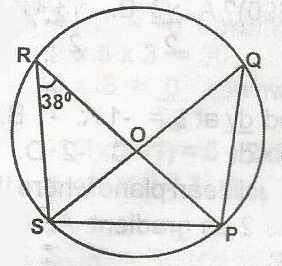
In the diagram, O is the centre of the circle. If SOQ is a diameter and < PRS is 38o, what is the value of < PSQ
- A. 148o
- B. 104o
- C. 80o
- D. 52o
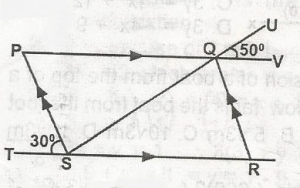
In the diagram, PQRS is a parallelogram. Find the value of < SQR
- A. 30o
- B. 50o
- C. 80o
- D. 100o
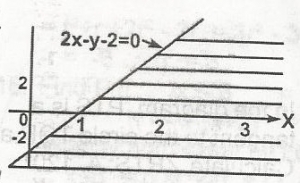
Find the inequality which represents the shaded portion in the diagram
- A. 2x - y - 2 \(\geq\) 0
- B. 2x - y - 2 \(\leq\) 0
- C. 2x - y - 2 < 0
- D. 2x - y - 2 > 0
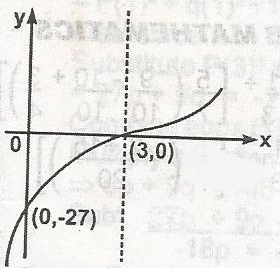
The equation of the graph is
- A. y = (x - 3)3
- B. y = (x + 3)3
- C. y = x3 - 27
- D. y = -x3 + 27
In a survey, it was observed that 20 students read newspapers and 35 read novels. If 40 of the students read either newspapers or novels, what is the probability of the students who read both newspapers and novels?
- A. \(\frac{1}{2}\)
- B. \(\frac{2}{3}\)
- C. \(\frac{3}{8}\)
- D. \(\frac{3}{11}\)
\(\begin{array}{c|c} x & 1 & 2 & 3 & 4 & 5 \\ \hline f & 2 & 1 & 2 & 1 & 2\end{array}\)
Find the variance of the frequency distribution above
- A. \(\frac{3}{2}\)
- B. \(\frac{9}{4}\)
- C. \(\frac{5}{2}\)
- D. 3
\(\begin{array}{c|c} \text{Class Interval} & 1 – 5 & 6 – 10 & 11 – 15 & 16 – 20 & 21 – 25 \\ \hline Frequency & 6 & 15 & 20 & 7 & 2\end{array}\)
Estimate the median of the frequency distribution above
- A. 10\(\frac{1}{2}\)
- B. 11\(\frac{1}{2}\)
- C. 12
- D. 13
Find the mean deviation of the set of numbers 4, 5, 9
- A. zero
- B. 2
- C. 5
- D. 6
\(\begin{array}{c|c} x & 1 & 2 & 3 & 4 & 5 \\ \hline f & y + 2 & y – 2 & 2y – 3 & y + 4 & 3y – 4\end{array}\)
This table shows the frequency distribution of a data if the mean is \(\frac{43}{14}\) find y
- A. 1
- B. 2
- C. 3
- D. 4
Evaluate \(\int^{1}_{-1}(2x + 1)^2 \mathrm d x\)
- A. 3\(\frac{2}{3}\)
- B. 4
- C. 4\(\frac{1}{3}\)
- D. 4\(\frac{2}{3}\)
Find the point (x, y) on the Euclidean plane where the curve y = 2x2 – 2x + 3 has 2 as gradient
- A. (1, 3)
- B. (2, 7)
- C. (0, 3)
- D. (3, 15)
If y = 3t3 + 2t2 – 7t + 3, find \(\frac{dy}{dt}\) at t = -1
- A. -1
- B. 1
- C. -2
- D. 2
What is the value of sin(-690)?
- A. \(\frac{\sqrt{3}}{2}\)
- B. -\(\frac{\sqrt{3}}{2}\)
- C. \(\frac{-1}{2}\)
- D. \(\frac{1}{2}\)
The angle of depression of a boat from the top of a cliff 10m high is 30. How far is the boat from the foot of the cliff?
- A. \(\frac{5√3m}{3}\)
- B. 5√3m
- C. 10√3m
- D. \(\frac{10√3m}{3}\)
If M(4, q) is the mid-point of the line joining L(p, -2) and N(q, p). Find the values of p and q
- A. P = 2, q = 4
- B. p = 3, q = 1
- C. p = 5, q = 3
- D. p = 6, q = 2
What is the locus of a point P which moves on one side of a straight line XY, so that the angle XPY is always equal to 90o?
- A. the perpendicular bisector of XY
- B. a right-angled triangle
- C. a circle
- D. a semi circle


