Mathematics JAMB, WAEC, NECO AND NABTEB Official Past Questions

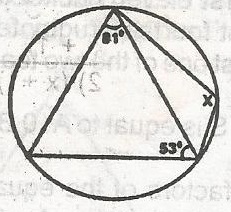
The mean and the range of the set of numbers 1, 20, 1.00, 0.90, 1.40, 0.80, 1.20 and 1.10 are me and r

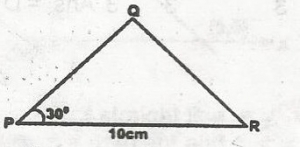
In the diagram, find PQ if the area of triangle PQR is 35cm\(^2\)

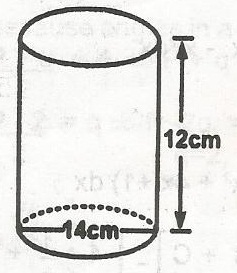
In the diagram, the base diameter is 14cm while the height is 12cm. Calculate the total surface area if the cylinder has both a base and a top.[\(\pi \frac{22}{7}\)]

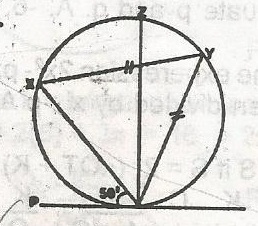
PT is a tangent to the circle TYZX. YT = YX and < PTX = 50^o. Calculate < TZY

Determine the value of x in the figure

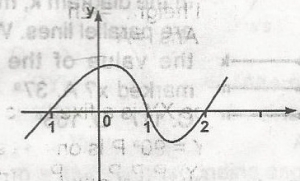
Use the graph of the curve y = f(x)to solve the inequality f(x) \(\leq\) 0

A die has four of it’s faces coloured white and the remaining two coloured black. What is the probability that when the die is thrown two consecutive time, the top face will be white in both cases?

Let p be a probability function on set S, where S = (a₁, a₂, a₃, a₄). Find P(a₁) if P(a₂) = \(\frac{1}{3}\), p(a₃) = \(\frac{1}{6}\) and p(a₄) = \(\frac{1}{5}\)

\(\begin{array}{c|c} \text{Class Interval} & Frequency & \text{Class boundaries} & Class Mid-point \\ \hline 1.5 – 1.9 & 2 & 1.45 – 1.95 & 1.7\\ 2.0 – 2.4 & 21 & 1.95 – 2.45 & 2.2\\ 2.5 – 2.9 & 4 & 2.45 – 2.95 & 2.7 \\ 3.0 – 2.9 & 15 & 2.95 – 3.45 & 3.2\\ 3.5 – 3.9 & 10 & 3.45 – 3.95 & 3.7\\ 4.0 – 4.4 & 5 & 3.95 – 4.45 & 4.2\\ 4.5 – 4.9 & 3 & 4.45 – 4.95 & 4.7\end{array}\)
The median of the distribution above is

\(\begin{array}{c|c} \text{Class Interval} & Frequency & \text{Class boundaries} & Class Mid-point \\ \hline 1.5 – 1.9 & 2 & 1.45 – 1.95 & 1.7\\ 2.0 – 2.4 & 1 & 1.95 – 2.45 & 2.2\\ 2.5 – 2.9 & 4 & 2.45 – 2.95 & 2.7 \\ 3.0 – 2.9 & 15 & 2.95 – 3.45 & 3.2\\ 3.5 – 3.9 & 10 & 3.45 – 3.95 & 3.7\\ 4.0 – 4.4 & 5 & 3.95 – 4.45 & 4.2\\ 4.5 – 4.9 & 3 & 4.45 – 4.95 & 4.7\end{array}\)
Find the mode of the distribution.

The variance of the scores 1, 2, 3, 4, 5 is

\(\begin{array}{c|c} class& 1 – 3 & 4 – 6 & 7 – 9\\ \hline Frequency & 5 & 8 & 5\end{array}\)
Find the standard deviation of the data using the table above

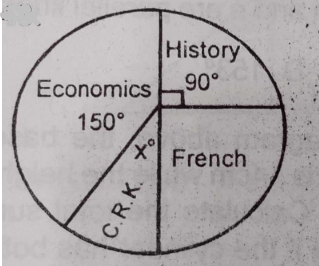
The pie chart shows the distribution of students in a secondary school class. If 30 students offered French, how many offered C.R.K?

\(\begin{array}{c|c} \text{Age in years} & 13 & 14 & 15 & 16 & 17 \\ \hline \text{No. of students} & 3 & 10 & 30 & 42 & 15\end{array}\)
The frequency distribution above shows the ages of students in a secondary school. In a pie chart constructed to represent the data, the angles corresponding to the 15 years old is

Find the area bounded by the curve y = 3x\(^2\) – 2x + 1, the ordinates x = 1 and x = 3 and the x-axis.

Two variables x and y are such that \(\frac{dy}{dx}\) = 4x – 3 and y = 5 when x = 2. Find y in terms of x

For what value of x is the tangent to the curve y = x\(^2\) – 4x + 3 parallel to the x-axis?

The derivative of cosec x is

A school boy lying on the ground 30m away from the foot of a water tank tower observes that the angle of elevation of the top of the tank 60^o. Calculate the height of the water tank.

P is on the locus of points equidiatant from two given points X and Y. UV is a straight line throuh Y parallel to the locus. If < PYU is 40°, find < XPY.

Two perpendicular lines PQ and QR intersect at (1, -1). If the equation of PQ is x – 2y + 4 = 0, find the equation of QR