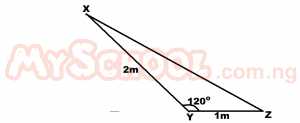
Find the length XZ in the triangle above.

Explanation

XY = z,

XZ = y,

YZ = x 

y\(^2\) = z\(^2\) + x\(^2\) - 2xz cos 120
y\(^2\) = 2\(^2\) + 1\(^2\) - 2 [2 * 1] cos 120
= 4 + 1 -2 x 2 -cos(180 - 120)
= 4 + 1 - 4 [-cos 60]
= 5 - 4 [-1/2]
= 5 + 2
y\(^2\)= 7
y = √7 m