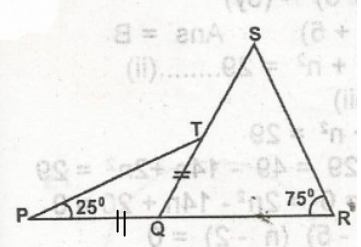
In the figure PQR a straight line segment, PQ = QT. Triangle PQT is an…

Mathematics JAMB 2001

In the figure PQR a straight line segment, PQ = QT. Triangle PQT is an isosceles triangle, < SRQ is 75º and < QPT IS 25º. Calculate the value of < RST

  • 50o
  • 25o
  • 55o checkmark
  • 45o

The correct answer is: C

Explanation

< T = \(\frac{x}{1}\) = 25o (PQ = QT)

< SQR = 2(25o) = 50o (sum of interior angle)

< Q + < R + < S = 180o

50o + 75o + < S = 180o = 125o + < S = 180o

< S = 180o - 125o = 55o

There is an explanation video available .

Previous Question Next Question

Leave A Comment