Evaluate \(\frac{2\sin 30 + 5\tan 60}{\sin 60}\), leaving your answer in surd form.
- A. \(\frac{2\sqrt{3}}{3} + 10\)
- B. \(\frac{3\sqrt{2} - 1}{5}\)
- C. \(\frac{3\sqrt{2} + 1}{5}\)
- D. \(\frac{2\sqrt{3}}{3} - 10\)
If \(\sin x = \frac{4}{5}\), find \(\frac{1 + \cot^2 x}{\csc^2 x – 1}\).
- A. \(\frac{13}{2}\)
- B. \(\frac{25}{9}\)
- C. \(\frac{3}{13}\)
- D. \(\frac{4}{11}\)
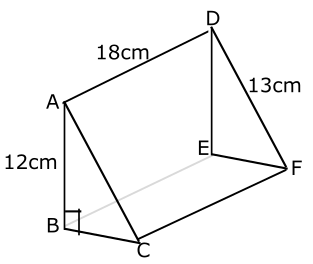
Calculate the volume of the regular three dimensional figure drawn above, where < ABC = 90° (a right- angled triangle).
- A. 394 cm\(^3\)
- B. 425 cm\(^3\)
- C. 268 cm\(^3\)
- D. 540 cm\(^3\)
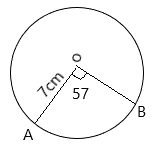
In the circle above, with centre O and radius 7 cm. Find the length of the arc AB, when < AOB = 57°.
- A. 5.32 cm
- B. 4.39 cm
- C. 7.33 cm
- D. 6.97 cm
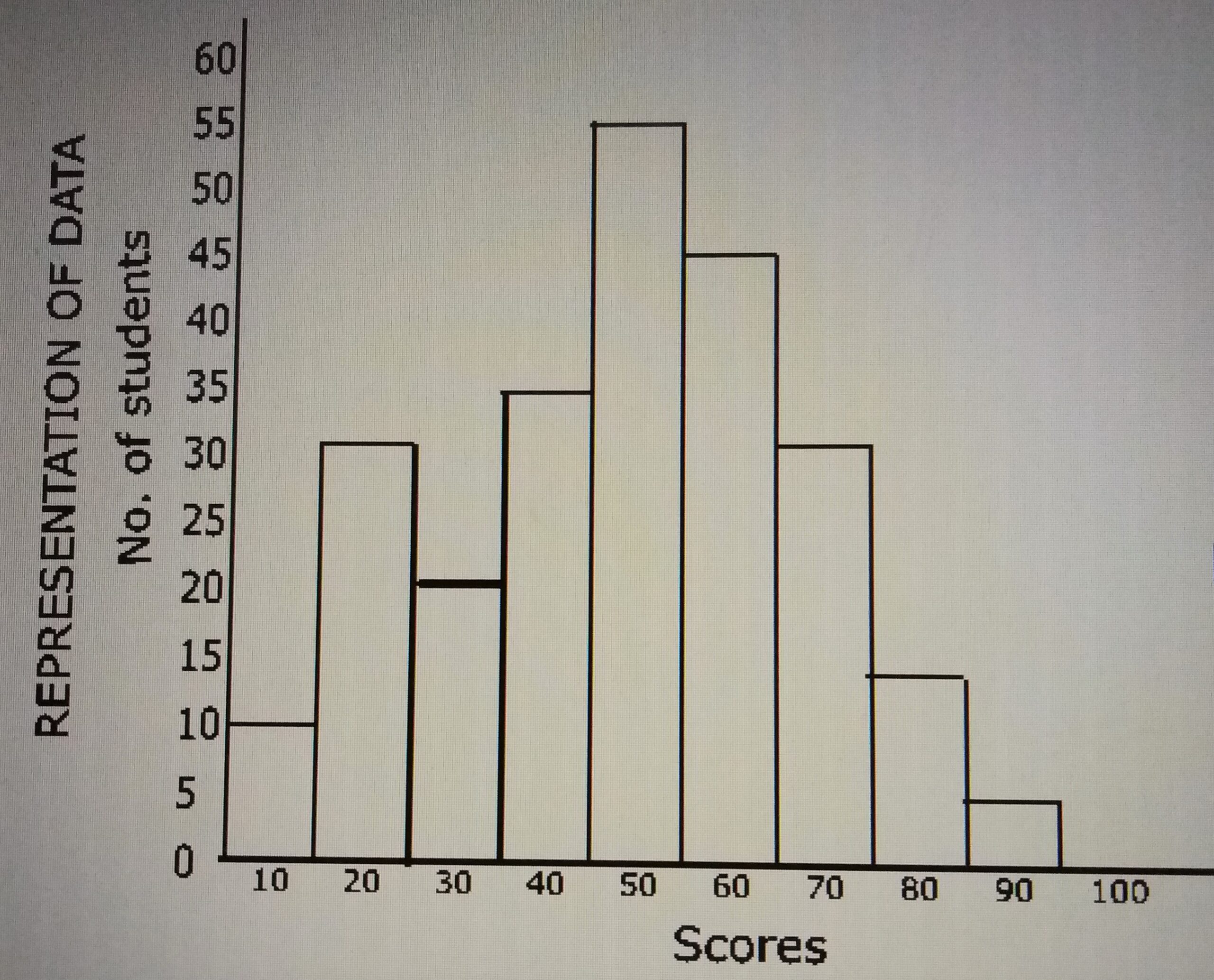
The histogram above represents the number of candidates who did Further Mathematics examination in a school. How many candidates scored more than 40?
- A. 100
- B. 79
- C. 150
- D. 90
| Marks | 1 | 2 | 3 | 4 | 5 |
| Frequency | 2y – 2 | y – 1 | 3y – 4 | 3 – y | 6 – 2y |
The table above is the distribution of data with mean equals to 3. Find the value of y.
- A. 5
- B. 2
- C. 3
- D. 6
Find the equation of a line perpendicular to the line 4y = 7x + 3 which passes through (-3, 1)
- A. 7y + 4x + 5 = 0
- B. 7y - 4x - 5 = 0
- C. 3y - 5x + 2 = 0
- D. 3y + 5x - 2 = 0
Find the distance between the points C(2, 2) and D(5, 6).
- A. 13 units
- B. 7 units
- C. 12 units
- D. 5 units
Differentiate \(\frac{2x}{\sin x}\) with respect to x.
- A. \(2 \cot x \sec x (1 + \tan x)\)
- B. \(2 \csc x - x \cot x\)
- C. \(2x \csc x + \tan x\)
- D. \(2\csc x(1 - x\cot x)\)
If y = 8x\(^3\) – 3x\(^2\) + 7x – 1, find \(\frac{\mathrm d^2 y}{\mathrm d x^2}\).
- A. 48x - 6
- B. 11x\(^2\) + 6x - 7
- C. 32x + 7
- D. 24x\(^2\) - 6x + 7
Given the matrix \(A = \begin{vmatrix} 3 & -2 \\ 1 & 6 \end{vmatrix}\). Find the inverse of matrix A.
- A. \(\begin{vmatrix} 6 & 2 \\ 1 & 6 \end{vmatrix}\)
- B. \(\begin{vmatrix} \frac{2}{11} & \frac{1}{12}\\ \frac{3}{20} & \frac{1}{10} \end{vmatrix}\)
- C. \(\begin{vmatrix} -3 & 2 \\ -1 & -6 \end{vmatrix}\)
- D. \(\begin{vmatrix} \frac{3}{10} & \frac{1}{10} \\ \frac{-1}{20} & \frac{3}{20}\end{vmatrix}\)
If \(\begin{vmatrix} 2 & -5 & 3 \\ x & 1 & 4 \\ 0 & 3 & 2 \end{vmatrix} = 132\), find the value of x.
- A. 5
- B. 8
- C. 6
- D. 3
If 2x\(^2\) + x – 3 divides x – 2, find the remainder.
- A. 7
- B. 3
- C. 5
- D. 6
Find the polynomial if given q(x) = x\(^2\) – x – 5, d(x) = 3x – 1 and r(x) = 7.
- A. 3x\(^3\) - 4x\(^2\) - 14x + 12
- B. 3x\(^2\) + 3x - 7
- C. 3x\(^3\) + 4x\(^2\) + 14x - 12
- D. 3x\(^2\) - 3x + 4
Determine the values for which \(x^2 – 7x + 10 \leq 0\)
- A. 2 \(\leq\) x \(\geq\) 5
- B. -2 \(\leq\) x \(\leq\) 3
- C. -2 \(\leq\) x \(\geq\) 3
- D. 2 \(\leq\) x \(\leq\) 5
Find the value of x for \(\frac{2 + 2x}{3} – 2 \geq \frac{4x – 6}{5}\)
- A. x \(\geq\) -5
- B. x \(\geq\) -1
- C. x \(\leq\) -1
- D. x \(\leq\) 3
Evaluate \(\frac{2\log_{3} 9 \times \log_{3} 81^{-2}}{\log_{5} 625}\)
- A. 4
- B. -32
- C. -8
- D. 16
Find the value of k in the equation: \(\sqrt{28} + \sqrt{112} – \sqrt{k} = \sqrt{175}\)
- A. \(\sqrt{28}\)
- B. 7
- C. 28
- D. \(\sqrt{7}\)
In a committee of 5, which must be selected from 4 males and 3 females. In how many ways can the members be chosen if it were to include 2 females?
- A. 144 ways
- B. 15 ways
- C. 185 ways
- D. 12 ways
If the universal set μ = {x : 1 ≤ x ≤ 20} and
A = {y : multiple of 3}
B = |z : odd numbers}
Find A ∩ B
- A. {1, 3, 6}
- B. {3, 5, 9, 12}
- C. {3, 9, 15}
- D. {2, 3, 9}
If the 3rd and 7th terms of a G.P are 9 and 1/9 respectively. Find the common ratio.
- A. \(\frac{1}{3}\)
- B. \(\frac{1}{9}\)
- C. \(\frac{2}{3}\)
- D. \(\frac{2}{9}\)


