The ages of students in a small primary school were recorded in the table below.
| Age | 5 – 6 | 7 – 8 | 9 -10 |
| Frequency | 29 | 40 | 38 |
Estimate the mean
- A. 7.7
- B. 7.5
- C. 7.8
- D. 7.6
Evaluate the following limit: \(lim_{x\to2} \frac {x^2 + 4x – 12}{x^2 – 2x}\)
- A. 4
- B. 8
- C. 0
- D. 2
At simple interest, a man made a deposit of some money in the bank. The amount in his bank account after 10 years is three times the money deposited. If the interest rate stays the same, after how many years will the amount be five times the money deposited?
- A. 15 years
- B. 25 years
- C. 20 years
- D. 30 years
Find the value of t, if the distance between the points P(–3, –14) and Q(t, –5) is 9 units.
- A. 3
- B. 2
- C. - 3
- D. - 2
If \(\frac {3 – \sqrt 3}{2 + \sqrt 3} = a + b\sqrt 3\), what are the values a and b?
- A. a = 9, b = -5
- B. a = 5, b = 9
- C. a = 9, b = 5
- D. a = -5, b = 9
Divide 1101001\(_{two}\) by 101\(_{two}\)
- A. 11101\(_{two}\)
- B. 111\(_{two}\)
- C. 10111\(_{two}\)
- D. 10101\(_{two}\)
If a car runs at a constant speed and takes 4.5 hrs to run a distance of 225 km, what time will it take to run 150 km?
- A. 2 hrs
- B. 4 hrs
- C. 3 hrs
- D. 1 hr
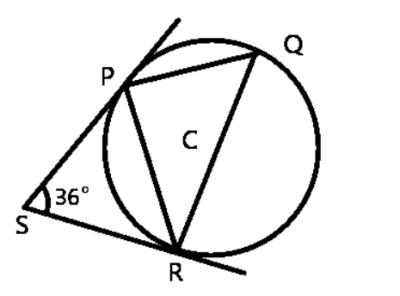
The diagram above is a circle with centre C. P, Q and S are points on the circumference. PS and SR are tangents to the circle. ∠PSR = 36\(^o\). Find ∠PQR
- A. 72\(^0\)
- B. 36\(^0\)
- C. 144\(^0\)
- D. 54\(^0\)
Solve for x: 3(x – 1) ≤ 2 (x – 3)
- A. x ≤ -3
- B. x ≥ -3
- C. x ≤ 3
- D. x ≥ 3
Make x the subject of the formula: y = \(\frac {3x – 9c}{4x + 5d}\)
- A. x = \(\frac {-(9c - 5dy)}{4y - 3}\)
- B. x = \(\frac {9c + 5dy}{4y - 3}\)
- C. x = \(\frac {9c - 5dy}{4y - 3}\)
- D. x = \(\frac {-(9c + 5dy)}{4y - 3}\)
The area A of a circle is increasing at a constant rate of 1.5 cm\(^2s^{-1}\). Find, to 3 significant figures, the rate at which the radius r of the circle is increasing when the area of the circle is 2 cm\(^2\).
- A. 0.200 cms\(^{-1}\)
- B. 0.798 cms\(^{-1}\)
- C. 0.300 cms\(^{-1}\)
- D. 0.299 cms\(^{-1}\)
The interior angle of a regular polygon is five times the size of its exterior angle. Identify the polygon.
- A. dodecagon
- B. enneadecagon
- C. icosagon
- D. hendecagon
The population of a village decreased from 1,230 to 1,040 due to breakout of an epidemic. What is the percentage decrease in the population?
- A. 15.44%
- B. 15.43%
- C. 15.42%
- D. 15.45%
Evaluate \(\int_0^1 4x – 6\sqrt[3] {x^2}dx\)
- A. - \(\frac{5}{8}\)
- B. - \(\frac{8}{5}\)
- C. \(\frac{8}{5}\)
- D. \(\frac{5}{8}\)
Let ‘*’ and ‘^’ be two binary operations such that a * b = a\(^2\)b and a ^ b = 2a + b. Find (-4 * 2) ^ (7 * -1).
- A. -49
- B. 64
- C. 113
- D. 15
Evaluate: 16\(^{0.16}\) × 16\(^{0.04}\) × 2\(^{0.2}\)
- A. 2
- B. 0
- C. 2\(^0\)
- D. \(\frac{1}{2}\)
How many different 8 letter words are possible using the letters of the word SYLLABUS?
- A. (8 - 1)!
- B. \(\frac{8!}{2!}\)
- C. \(\frac{8!}{2! 2!}\)
- D. 8!


