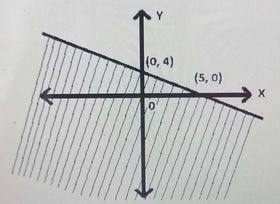
Which inequality describes the graph above?

Explanation

First, we find the equation of the boundary line using the two intercepts.The slope is

m = \(\frac{4 - 0}{0 - 5} = {4}{5}\)

The y-intercept is 4

The slope-intercept form of the equation is therefore

y = -\(\frac{4}{5} x + 4\)

\(\implies y + \frac{4}{5} x = 4\)

Multiply both sides by \(\frac{5}{4}\)

\(\implies\frac{5}{4}(y +\frac{4}{5} x) = 4\times\frac{5}{4}\)

\(\implies\frac{5}{4} y + x = 5\)

Multiply both sides by 4

⇒ \(5y + 4x = 20\)

The inequality is therefore either \(5y + 4x ≤ 20\) or \(5y + 4x ≥ 20.\)

Using the test point (0, 0) -The origin

⇒ 5(0) + 4(0) ≤ 20

⇒ 0 ≤ 20 (True)

∴ The inequality is \(5y + 4x ≤ 20\)

There is an explanation video available .