The area of a trapezium is 200 cm\(^2\). Its parallel sides are in the ratio 2 : 3 and the perpendicular distance between them is 16 cm. Find the length of each of the parallel sides.
-
10 cm and 15 cm
- 8 cm and 12 cm
- 6 cm and 9 cm
- 12 cm and 18 cm
The correct answer is: A
Explanation
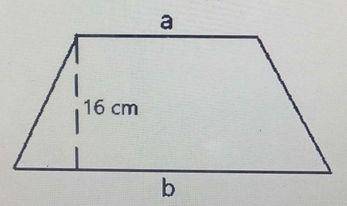
Area of trapezium = \(\frac{1}{2}(a + b) h\)
⇒ \(\frac{1}{2} (a + b)\times 16 = 200\)
⇒ 8(a + b) = 200
⇒ a + b = \(\frac{200}{8}\) = 25 -----(i)
⇒ a : b = 2 : 3
⇒ \(\frac{a}{b} = \frac{2}{3}\)
⇒ 3a = 2b
⇒ a = \(\frac{2b}{3}\) -------(ii)
Substitute \(\frac{2b}{3}\) for a in equation (i)
⇒ \(\frac{2b}{3}\) + b = 25
\(\frac{5b}{3}\) = 25
⇒ b = 25 ÷ \(\frac{5}{3} = 25\times\frac{3}{5} = 15cm\)
From equation (ii)
⇒ a = \(\frac{2 \times 15}{3} = 2\times5 = 10cm\)
∴ Lengths of each parallel sides are 10cm and 15cm
There is an explanation video available .