A circle has a radius of 13 cm with a chord 12 cm away from the centre of the circle. Calculate the length of the chord.
- 16 cm
- 8 cm
- 5 cm
-
10 cm
The correct answer is: D
Explanation
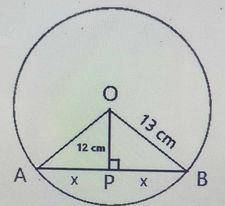
|AP| = |PB| = \(x\) (The perpendicular to a chord bisects the chord if drawn from the center of the circle.)
From ∆OPB
Using Pythagoras theorem
⇒ \(13^2 = 12^2 + x^2\)
⇒ \(169 = 144 + x^2\)
⇒ \(169 - 144 = x^2\)
⇒ \(x^2 = 25\)
⇒ \(x = \sqrt25 = 5 cm\)
∴ Length of the chord |AB| = \(x + x = 5 + 5 = 10 cm\)
There is an explanation video available .