The table below shows the frequency distribution of the marks of 800 candidates in an examination.
| Marks | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Freq | 10 | 40 | 80 | 140 | 170 | 130 | 100 | 70 | 40 | 20 |
(a) (i) Construct a cumulative frequency table ; (ii) Draw the Ogive ; (iii) Use your ogive to determine the 50th percentile.
(b) The candidates that scored less than 25% are to be withdrawn from the institution, while those that scored than 75% are to be awarded scholarship. Estimate the number of students that will be retained, but will not enjoy the award.
Using a ruler and a pair of compasses only,
(a) construct (i) a triangle ABC such that |AB| = 5cm, |AC| = 7.5cm and < CAB = 120° ; (ii) the locus \(L_{1}\) of points equidistant from A and B ; (iii) the locus \(L_{2}\) of points equidistant from Ab and AC, which passes through the triangle ABC.
(b) Label the point P where \(L_{1}\) and \(L_{2}\) intersect;
(c) Measure |CP|.
(a) Prove that the sum of the angles in a triangle is two right angles.
(b) In a triangle LMN, the side NM is produced to P and the bisector of < LNP meets ML produced at Q. If < LMN = 46°, and < MLN = 80°, calculate < LQN, stating clearly your reasins.
Two towns K and Q are on the parallel of latitude 46°N. The longitude of town K is 130°W and that of town Q is 103°W. A third town P also on latitude 46°N is on longitude 23°E, Calculate:
(i) the length of the parallel of latitude 46°N, to the nearest 100km;
(ii) the distance between K and Q, correct to the nearest 100km;
(iii) the distance between Q and P measured along the parallel of latitude, to the nearest 10km.
[Take \(\pi = 3.142\); Radius of the earth = 6400km]
The table below is for the relation \(y = 2 + x – x^{2}\)
| x | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| y | -4 | -1.75 | 0 | 1.25 | 2 | 2.25 | 2 | 1.25 | 0 | -1.75 | -4 |
(a) Using a scale of 2cm to 1 unit on each axis, draw the graph of the relation in the interval \(-2 \leq x \leq 3\).
(b) From your graph, find the greatest value of y and the value of x for which this occurs.
(c) Using the same scale and axes, draw the graph of \(y = 1 – x\)
(d) Use your graphs to solve the equation \(1 + 2x – x^{2} = 0\)
Illustrate the following on graph paper and shade the region which satisfies all the three inequalities at the same time :
\(- x + 5y \leq 10 ; 3x – 4y \leq 8\) and \(x > -1\).
(a) The subsets A, B and C of a universal set are defined as follows :
A = {m, a, p, e} ; B = {a, e, i, o, u} ; C = {l, m, n, o, p, q, r, s, t, u}. List the elements of the following sets.
(i) \(A \cup B\) ; (ii) \(A \cup C\) ; (iii) \(A \cup (B \cap C)\).
(b) Out of the 400 students in the final year in a Senior Secondary School, 300 are offering Biology and 190 are offering Chemistry.
(i) How many students are offering both Biology and Chemistry, if only 70 students are offering neither Biology nor Chemistry? (ii) How many students are offering at least one of Biology or Chemistry?
A sector of a circle of radius 7cm subtending an angle of 270° at the centre of the circle is used to form a cone.
(a) Find the base radius of the cone.
(b) Calculate the area of the base of the cone to the nearest square centimetre.
[Take \(\pi = \frac{22}{7}\)]
In a certain school, the lesson periods for each week are as itemised below: English 10, Mathematics 7, Biology 3, Statistics 4, Ibo 3, others 9. Draw a pie chart to illustrate this information.
(a) Given that \(\sin \alpha = 0.3907\), use tables to find the value of : (i) \(\tan \alpha\) ; (ii) \(\cos \alpha\).
(b) A ladder of length 4.5m leans against a vertical wall making an angle of 50° with the horizontal ground. If the bottom of a window is 4m above the ground, what is the distance between the top of the ladder and the bottom of the window? (Answer correct to the nearest cm)
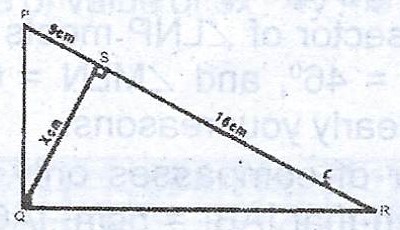
In the diagram, < PQR = < PSQ = 90°, |PS| = 9 cm, |SR| = 16 cm and |SQ| = x cm.
(a) Find the value of x using a trigonometric ratio.
(b) Calculate : (i) the size of < QRS to the nearest degree; (ii) |PQ|.
The number of items produced by a company over a five- year period is given below:
| Year | 1978 | 1979 | 1980 | 1981 | 1982 |
| No produced | 4100 | 2500 | 1500 | 1800 | 9200 |
(i) Plot a bar chart for this information; (ii) What is the average production for the five- year period.
The surnames of 40 children in a class arranged in alphabetical order. 16 of the surnames begins with O and 9 of the surname begins with A, 14, of the letters of the alphabet do not appear as the first letter of a surname
If more than one surname begins with a letter besides A and O, how may surnames begin with that letter
- A. 2
- B. 3
- C. 4
- D. 5
- E. 6
The surnames of 40 children in a class arranged in alphabetical order. 16 of the surnames begins with O and 9 of the surname begins with A, 14, of the letters of the alphabet do not appear as the first letter of a surname
What is the probability that the surname of a child picked at random from the class begins with either O or A?
- A. 5/8
- B. 7/8
- C. 9/16
- D. 14/25
- E. 39/40
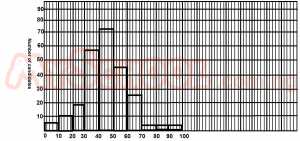
The histogram below shows the number of candidates, in thousands, obtaining given ranges of marks in a State examination. How many candidates scored at most 30%?
- A. 15,000
- B. 20,000
- C. 25,000
- D. 35,000
- E. 60,000
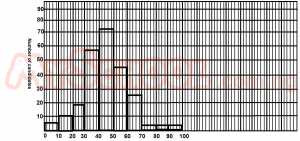
The histogram below shows the number of candidates, in thousands, obtaining given ranges of marks in a State examination. Find the total number of candidates that sat for the examination
- A. 80,000
- B. 120,000
- C. 250,000
- D. 260,000
- E. 270,000
If Q = (all perfect squares less than 30) and P = (all odd numbers from 1 to 10). Find Q ∩ P.
- A. (1, 4, 9, 16, 25)
- B. (1, 3, 4, 5, 7, 9, 16, 25)
- C. (1, 3, 5, 7, 9)
- D. (1, 9)
- E. Φ
Cotonou and Niamey are on the same line of longitude and Niamey is 7o north of Cotonou. If the radius of the earth is 6400km, how far is Niamey north of Cotonou along the line of longitude, correct to the nearest kilometer? [Take π = 22/7]
- A. 391km
- B. 503km
- C. 782km
- D. 1006km
- E. 2012km
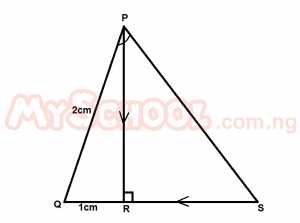
In the diagram above, PR is perpendicular from P to QS, PQ = 2cm, QR = 1cm and PR = RS. what is the size of the angle QPS?
- A. 135o
- B. 105o
- C. 90o
- D. 75o
- E. 60o
A rope of length 18m is used to form a sector of a circle of radius 3.5m on a school playing field. What is the size of the angle of the sector, correct to the nearest degree?
- A. 33o
- B. 40o
- C. 90o
- D. 180o
- E. 270o
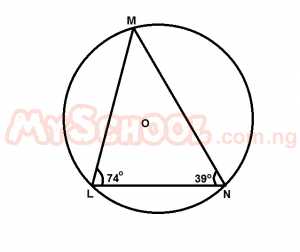
In the diagram above, O is the centre of the circle through points L, M and N, if ∠MLN = 74o and ∠MNL = 39o, calculate ∠LON.
- A. 67o
- B. 100o
- C. 113o
- D. 126o
- E. 134o


