(a) Given that \(\sin \alpha = 0.3907\), use tables to find the value of : (i) \(\tan \alpha\) ; (ii) \(\cos \alpha\).
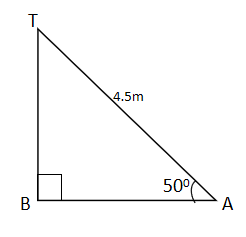
(b) A ladder of length 4.5m leans against a vertical wall making an angle of 50° with the horizontal ground. If the bottom of a window is 4m above the ground, what is the distance between the top of the ladder and the bottom of the window? (Answer correct to the nearest cm)
Explanation
(a) Given \(\sin \alpha = 0.3907\)
From the sine table, \(\alpha = 23°\)
(i) \(\tan \alpha = \tan 23° = 0.4245\)
(ii) \(\cos \alpha = \cos 23° = 0.9205\)
(b) Let T be the top of the ladder and B, the bottom of the vertical wall.
From the figure, above \(\sin 50° = \frac{BT}{4.5m}\)
\(BT = 4.5 \sin 50° = 4.5 \times 0.7660\)
\(BT = 3.447m\)
Distance between the top of the ladder and bottom of the window
= \(4 - 3.447 = 0.553m\)
= \( 0.553m \times 100\)
= \(55.3 cm\)

