(a) The subsets A, B and C of a universal set are defined as follows :
A = {m, a, p, e} ; B = {a, e, i, o, u} ; C = {l, m, n, o, p, q, r, s, t, u}. List the elements of the following sets.
(i) \(A \cup B\) ; (ii) \(A \cup C\) ; (iii) \(A \cup (B \cap C)\).
(b) Out of the 400 students in the final year in a Senior Secondary School, 300 are offering Biology and 190 are offering Chemistry.
(i) How many students are offering both Biology and Chemistry, if only 70 students are offering neither Biology nor Chemistry? (ii) How many students are offering at least one of Biology or Chemistry?
Explanation
(a) A = {m, a, p, e}; B = {a, e, i, o, u} ; C = {l, m, n, o, p, q, r, s, t, u}
(i) \(A \cup B = {a, e, i, m, o, p, u}\)
(ii) \(A \cup C = {a, e, l, m, n, o, p, q, r, s, t, u}\)
(iii) \(A \cup (B \cap C)\)
\(B \cap C = {o, u}\)
\(A \cup (B \cap C) = {m, a, p, e, o, u}\)
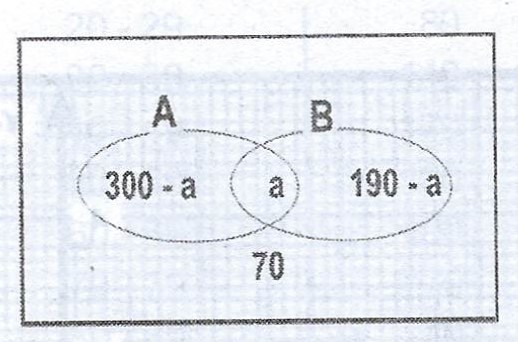
Biology students = n(B) = 190
Chemistry students = n(A) = 300
Let \(n(A \cap B) = a\)
(i) From the Venn diagram,
\((300 - a) + a + (190 - a) + 70 = 400\)
\(560 - a = 400 \implies a = 160\)
\(\therefore\) 160 students offer both Biology and Chemistry.
(ii) Students offering at least one of Biology and Chemistry
= \(n(A) + n(B) + n(A \cap B)\)
= \((300 - 160) + (190 - 160) + 160\)
= \(140 + 30 + 160\)
= 330 students
330 students offer at least one of Biology and Chemistry.

