Two towns K and Q are on the parallel of latitude 46°N. The longitude of town K is 130°W and that of town Q is 103°W. A third town P also on latitude 46°N is on longitude 23°E, Calculate:
(i) the length of the parallel of latitude 46°N, to the nearest 100km;
(ii) the distance between K and Q, correct to the nearest 100km;
(iii) the distance between Q and P measured along the parallel of latitude, to the nearest 10km.
[Take \(\pi = 3.142\); Radius of the earth = 6400km]
Explanation
(i) 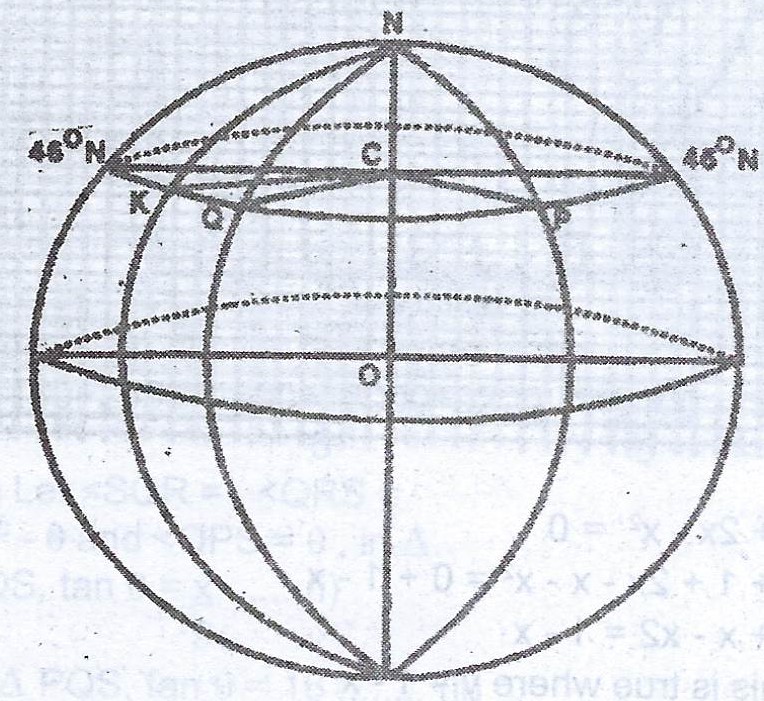
The length of the parallel of latitude 46°N = \(2 \pi R \cos 46°\)
= \(2 \times 3.142 \times 6400 \times 0.6947\)
= \(27,939.167 km \approxeq 28000 km\) (to the nearest 100km)
(ii) 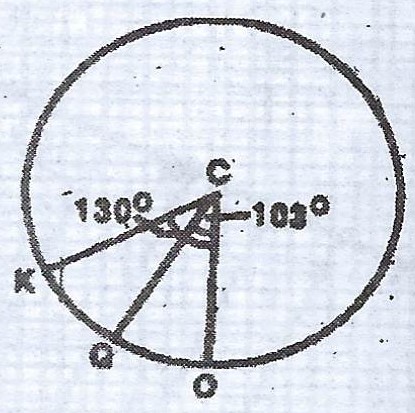
Longitudinal difference between K and Q = 130° - 103° = 27°
Distance between K and Q = length of arc KQ
= \(\frac{27}{360} \times 2 \times 3.142 \times 6400 \times \cos 46°\)
= \(2,095.31 km \approxeq 2100km\) (to the nearest 100km)
(iii) 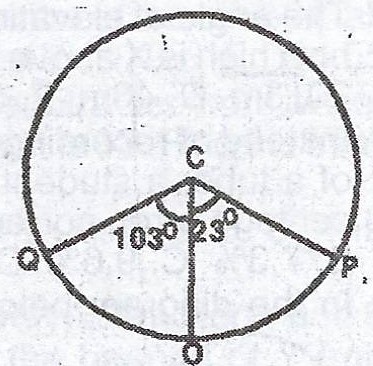
Longitudinal difference between Q and P = 103° + 23° = 126°
Distance between Q and P = \(\frac{126}{360} \times 2 \times 3.142 \times 6400 \times \cos 46°\)
= \(9778.12 km \approxeq 9780 km\) (to the nearest 10km)

