(a) Prove that the sum of the angles in a triangle is two right angles.
(b) In a triangle LMN, the side NM is produced to P and the bisector of < LNP meets ML produced at Q. If < LMN = 46°, and < MLN = 80°, calculate < LQN, stating clearly your reasins.
Explanation
(a) Given any \(\Delta\) ABC,
Required: That < A + < B + < C = 180°.
Construction : Draw CP // BA and produce BC to Q.

Proof: Using the above figure,
\(a_{1} = a_{2}\) (alternate angles)
\(b_{1} = b_{2}\) (corresponding angles)
\(a_{1} + b_{1} + c = 180°\) (angles on a straight line)
\(\therefore a_{2} + b_{2} + c = 180°\)
\(< A + < B + < C = 180°\) (proved)
(b) 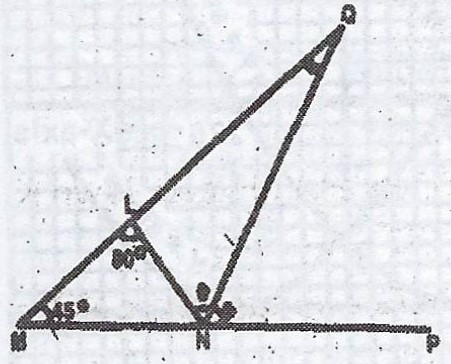
< LNP = 46° + 80° = 126° (exterior angles of triangle LMN)
\(\theta = \frac{126°}{2} = 63°\) (bisector divides into 2 equal halves)
\(< MLN = 180° - 80° = 100°\) (angles on a straight line)
\(< LQN = 180° - (63° + 100°) = 17°\)

