Mathematics JAMB, WAEC, NECO AND NABTEB Official Past Questions

(a) Derive the smallest equation whose coefficients are integers and which has roots of \(\frac{1}{2}\) and -7. 

(b) Three years ago, a father was four times as old as his daughter is now. The product of their present ages is 430. Calculate the ages of the father and daughter. 

(a) Triangle PQR is right-angled at Q. PQ = 3a cm and QR = 4a cm. Determine PR in terms of a. 

(b) Ayo travels a distance of 24km from X on a bearing of 060° to Y. He then travels a distance of 18km to a point Z  and Z is 30km from X.

(i) Draw the diagram to show the positions of X, Y and Z ; (ii) What is the bearing of Z from Y ; (iii) Calculate the bearing of X from Z.

(a) A pair of fair dice each numbered 1 to 6 is tossed. Find the probability of getting a sum of at least 9.

(b) If the probability that a civil servant owns a car is \(\frac{1}{6}\), find the probability that:

(i) two civil servants, A and B, selected at random each owns a car ; (ii) of two civil servants, C and D selected at random, only one owns a car ; (iii) of three civil servants, X, Y and Z, selected at random, only one owns a car.

(a) In an A.P, the difference between the 8th and 4th terms is 20 and the 8th term is \(1\frac{1}{2}\) times the 4th term. What is the:

(i) common difference ; (ii) first term of the sequence?

(b) The value of a machine depreciates each year by 5% of its value at the beginning of that year. If its value when new on 1st January 1980 was N10,250.00, what was its value in January 1989 when it was 9 years old? Give your answer correct to three significant figures.

(a) (i) Prove that the angle which an arc of a circle subtends at the centre is twice that which it subtends at any point on the remaining part of the circumference.

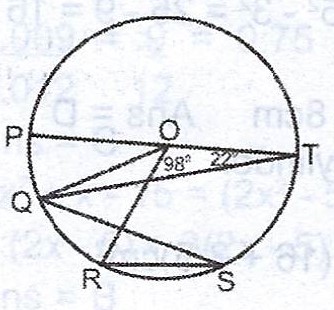
(ii) In the diagram above, O is the centre of the circle and PT is a diameter. If < PTQ = 22° and < TOR = 98°, calculate < QRS.

(b) ABCD is a cyclic quadrilateral and the diagonals AC and BD intersect at H. If < DAC = 41° and < AHB = 70°, calculate < ABC.

When a stone is thrown vertically upwards, its distance d metres after t seconds is given by the formula \(d = 60t – 10t^{2}\). Draw the graph of \(d = 60t – 10t^{2}\) for values of t from 1 to 5 seconds using 2cm to 1 unit on the t- axis and 2cm to 20 units on the d- axis.

(a) Using your graph, (i) how long does it take to reach a height of 70 metres? (ii) determine the height of the stone after 5 seconds. (iii) after how many seconds does it reach its maximum height.

(b) Determine the slope of the graph when t = 4 seconds.

(a)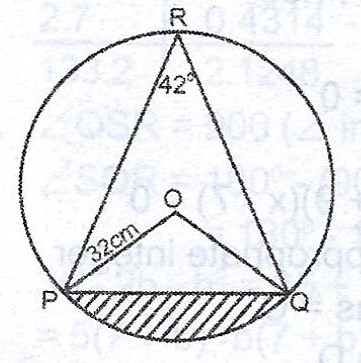 

In the diagram, O is the centre of the circle radius 3.2cm. If < PRQ = 42°, calculate, correct to two decimal places, the area of the:

(i) minor sector POQ ; (ii) shaded part.

(b) If the sector POQ in (a) is used to form the curved surface of a cone with vertex O, calculate the base radius of the cone, correct to one decimal place.

(a) If \(\cos \alpha = 0.6717\), use mathematical tables to find (i) \(\alpha\) ; (ii) \(\sin \alpha\)

(b) The angle of depression of a point P on the ground, from the top T of a building is 23.6°. If the distance of P from the foot of the building is 50m, calculate the height of the building, correct to the nearest metre.

Using a ruler and a pair of compasses only, construct a triangle ABC, given that |AB| = 8.4cm, |BC| = 6.5cm and < ABC = 30°. Construct the locus: 

(a) \(l_{1}\) of points equidistant from AB and BC, and within the angle ABC;

(b) \(l_{2}\) of points equidistant from B and C. Locate the point of intersection P of \(l_{1}\) and \(l_{2}\). Measure |AP|. 

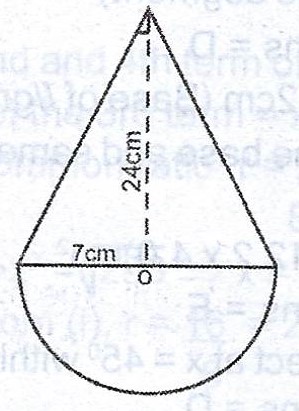
The diagram shows a wooden structure in the form of a cone, mounted on a hemispherical base. The vertical height of the cone is 24cm and the base height 7cm. Calculate, correct to three significant figures, the surface area of the structure. [Take \(\pi = \frac{22}{7}\)].

The table shows the weights, to the nearest kilogram, of twelve students in a Further Mathematics class

(a) Draw a bar chart to illustrate the above information;

(b) What is (i) the mode; (ii) the median of the distribution?

(c) Calculate the mean weight correct to the nearest kilogram.

(a) Without using Mathematical tables, find x, given that \(6 \log (x + 4) = \log 64\)

(b) If \(U = {1, 2, 3,4, 5, 6, 7, 8, 9, 10}, X = {1, 2, 4, 6, 7, 8, 9}, Y = {1, 2, 3, 4, 7, 9}\) and \(Z = {2, 3, 4, 7, 9}\). What is \(X \cap Y \cap Z’ \)?

In an A.P the first term is 2, and the sum of the 1st and the 6th term is 161/2. What is the 4th term

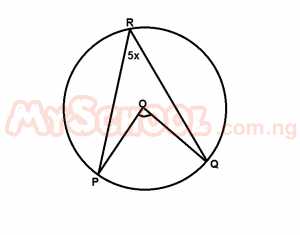
In the diagram, O is the center of the circle, If ∠POQ = 80^o and ∠PRQ = 5x, find the value of x.

What is the probability that 3 customers waiting in a bank will be served in the sequence of their arrival at the bank

sinθ = 1/2 and cosθ = -√3/2, what is the value of θ?

Given that logp = 2 logx + 3logq, which of the following expresses p in terms of x and q?

Solve for x: (x² + 2x + 1) = 25

The angle of depression of a point on the ground from the top of a building is 20.3^o. If the foot of the building is 40m, calculate the height of the building, correct to one decimal place

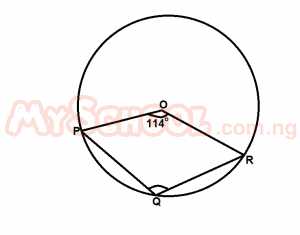
In the diagram above, O is the center of the circle. If ∠POR = 114^o, calculate ∠PQR

Calculate and correct to three significant figures, the length of an arc subtends an angle of 70^o at the center of the circle radius 4cm. [Take π = 22/7]