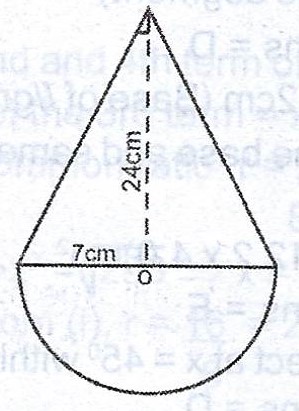
The diagram shows a wooden structure in the form of a cone, mounted on a hemispherical base. The vertical height of the cone is 24cm and the base height 7cm. Calculate, correct to three significant figures, the surface area of the structure. [Take \(\pi = \frac{22}{7}\)].
Explanation
Let the slant height = L ; height = 24cm ; r = 7cm.
\(\therefore L^{2} = 24^{2} + 7^{2} = 576 + 49 = 625\)
\(L = \sqrt{625} = 25cm\)
Surface area of the structure = Area of cone + Area of hemisphere
= \(\pi r L + 2 \pi r^{2} = \pi r (L + 2r)\)
= \(\frac{22}{7} \times 7 (25 + 2(7))\)
= \(22 \times 39 = 858 cm^{2}\)

