(a) If \(\cos \alpha = 0.6717\), use mathematical tables to find (i) \(\alpha\) ; (ii) \(\sin \alpha\)
(b) The angle of depression of a point P on the ground, from the top T of a building is 23.6°. If the distance of P from the foot of the building is 50m, calculate the height of the building, correct to the nearest metre.
Explanation
(a) (i) Given \(\cos \alpha = 0.6717\)
\(\alpha = \cos^{-1} 0.6717 = 47.8°\)
(From cosine of angle table)
(ii) \(\sin 47.8° = 0.7408\)
(b) 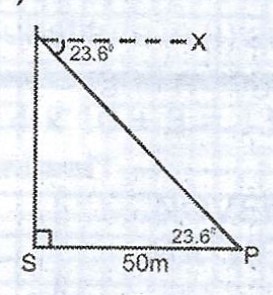
From the diagram, \(< BPT = < PTR = 23.6°\)
\(\therefore |BT| = |BP| \tan 23.6°\)
= \(50 \tan 23.6° = 50 \times 0.4369\)
= \(21.8469 m\)
\(\therefore\) The height of the building = 22m (to the nearest metre).

