(a) 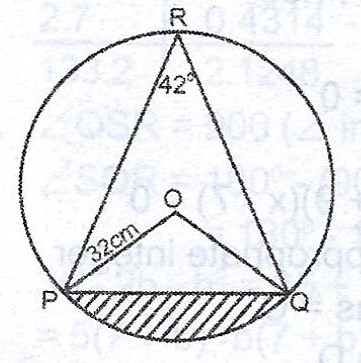
In the diagram, O is the centre of the circle radius 3.2cm. If < PRQ = 42°, calculate, correct to two decimal places, the area of the:
(i) minor sector POQ ; (ii) shaded part.
(b) If the sector POQ in (a) is used to form the curved surface of a cone with vertex O, calculate the base radius of the cone, correct to one decimal place.
Explanation
(a) (i) Area of minor segment POQ = \(\frac{84}{360} \times \frac{22}{7} \times (3.2)^{2}\)
= \(\frac{11 \times 10.24}{15}\)
= \(7.5093 cm^{2} \approxeq 7.51 cm^{2}\) (2 decimal places)
(ii) Area of \(\Delta\) in POQ = \(\frac{1}{2} \times 3.2 \times 3.2 \times \sin 84°\)
= \(\frac{127.296}{25} = 5.0918 cm^{2}\)
Area of segment PQ (shaded part) = Area of sector POQ - Area of triangle
= \(7.5093 cm^{2} - 5.0918 cm^{2} = 2.4175 cm^{2}\)
\(\approxeq 2.42 cm^{2}\)
(b) Area of sector POQ = Curved surface area of the cone
\(7.5093 cm^{2} = \pi rl\)
where r = base radius, L = slant height = 3.2cm
\(7.5093 = \frac{22}{7} \times r \times 3.2 = \frac{70.4r}{7}\)
\(70.4r = 7.5093 \times 7 \implies r = \frac{7.5093 \times 7}{70.4} = 0.7467 cm\)
\(\approxeq 0.7cm\)

