When a stone is thrown vertically upwards, its distance d metres after t seconds is given by the formula \(d = 60t – 10t^{2}\). Draw the graph of \(d = 60t – 10t^{2}\) for values of t from 1 to 5 seconds using 2cm to 1 unit on the t- axis and 2cm to 20 units on the d- axis.
(a) Using your graph, (i) how long does it take to reach a height of 70 metres? (ii) determine the height of the stone after 5 seconds. (iii) after how many seconds does it reach its maximum height.
(b) Determine the slope of the graph when t = 4 seconds.
Explanation
Table of values of \(d = 60t - 10t^{2}\)
| t | 1 | 2 | 3 | 4 | 5 |
| \(60t\) | 60 | 120 | 180 | 240 | 300 |
| \(- 10t^{2}\) | -10 | -40 | -90 | -160 | -250 |
| d | 50 | 80 | 90 | 80 | 50 |
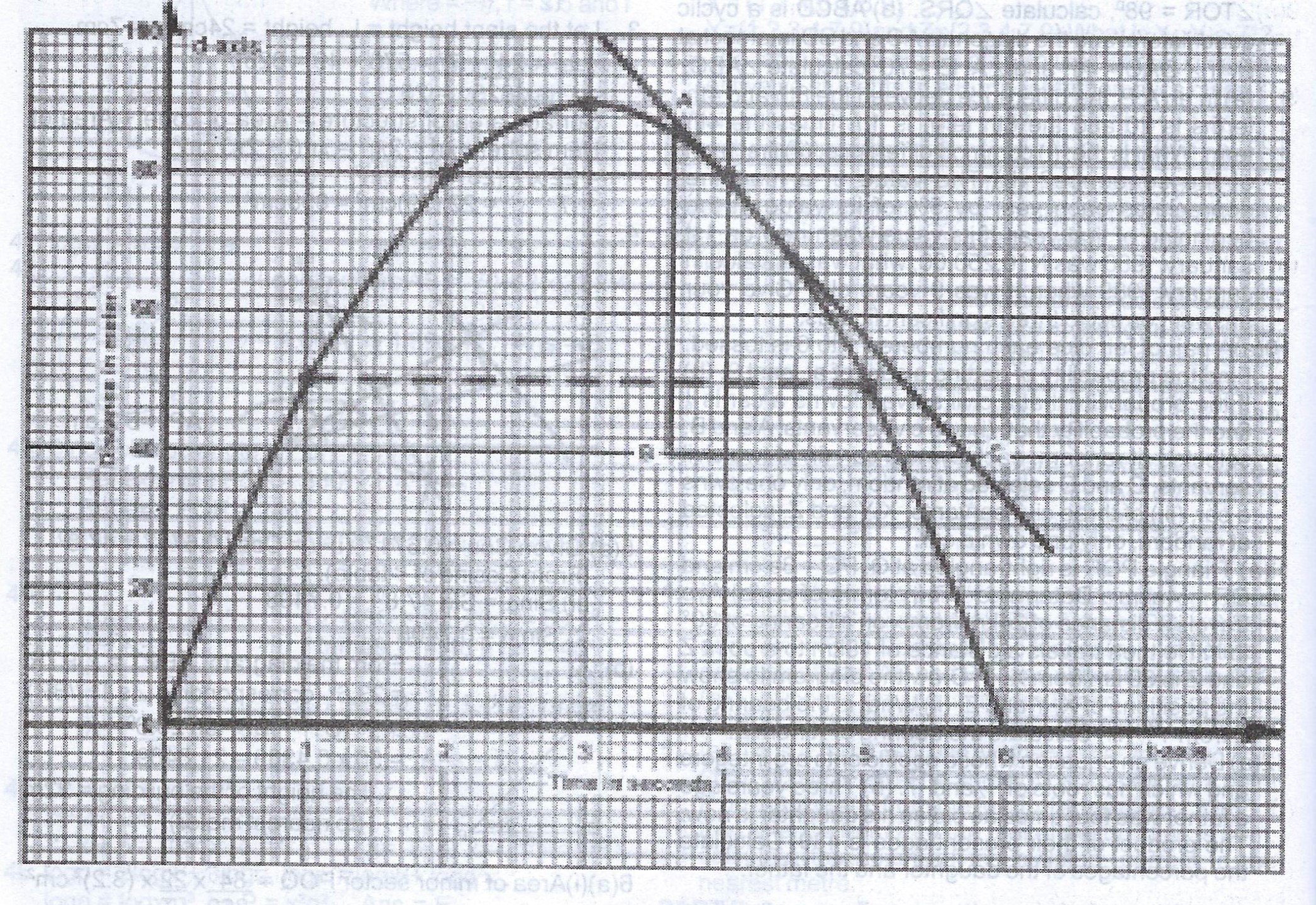
(a)(i) It takes 1.6 seconds to reach a height of 70 metres.
(ii) Height of stone at 5 seconds was 50 metres but after 5 seconds, d < 50 metres.
(iii) It reaches its maximum height after 2.9 seconds.
(b) From the graph, the gradient of the slope = \(\frac{AB}{BC}\)
= \(\frac{56}{2.8} = 20 m/s\)
But it is a negative slope, hence the slope = -20 m/s.

