(a) (i) Prove that the angle which an arc of a circle subtends at the centre is twice that which it subtends at any point on the remaining part of the circumference.
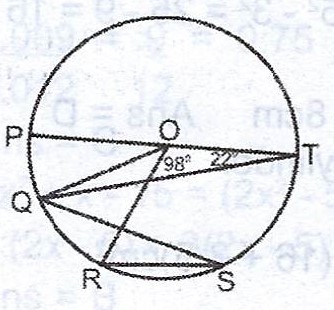
(ii) In the diagram above, O is the centre of the circle and PT is a diameter. If < PTQ = 22° and < TOR = 98°, calculate < QRS.
(b) ABCD is a cyclic quadrilateral and the diagonals AC and BD intersect at H. If < DAC = 41° and < AHB = 70°, calculate < ABC.
Explanation
(a)(i) 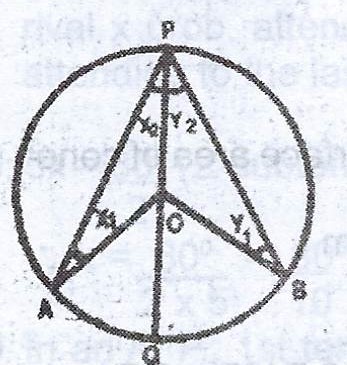
Given a circle APB with centre O.
To prove that < AOB = 2 < APB.
Construction: Draw PO and produce it to Q.
Proof : Referring to the lettering in the figure, |OA| = |OB| (radius)
\(\therefore x_{1} = x_{2}\) (base angles of isosceles triangle)
\(< AOQ = x_{1} + x_{2}\) (exterior angles of triangle AOP)
\(\therefore < AOQ = 2x_{2} (x_{1} = x_{2})\)
Similarly, \(< BOQ = 2y_{2}\)
\(< AOB = < AOQ + < BOQ \)
Hence, \(< AOB = 2x_{2} + 2y_{2} = 2(x_{2} + y_{2})\)
= \(2 \times < APB\)
(ii) 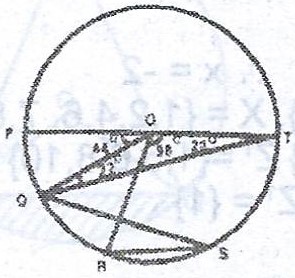
From the figure, \(|OQ| = |QT|\) (radius)
\(< OQT = 22° = < QTO\) (base angles of isosceles triangle)
\(\therefore < POQ = 44° \) (exterior angle of \(\Delta\) QOT)
\(< QOR = 180° - (44° + 98°) = 180° - 142° = 38°\) (Angles on a straight line)
\(< QOR = 2 \times < QSR = 38°\)
\(\therefore < QSR = \frac{38°}{2} = 19°\)
(b) 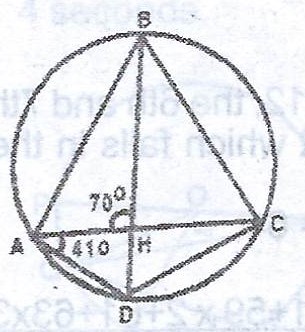
\(< BHC = (180° - 70°) = 110°\) (angle on a straight line)
\(< DAC = 41° = < DBC\) (angles on the same segment)
But \(< DBC = < HBC\)
\(< AHB = < HBC + < HCB \) (exterior angles of \(\Delta\) BHC)
\(70° = 41° + < HCB \implies < HCB = 70° - 41° = 29°\)
\(< ACB = < HCB = 29°\)

