(a) Triangle PQR is right-angled at Q. PQ = 3a cm and QR = 4a cm. Determine PR in terms of a.
(b) Ayo travels a distance of 24km from X on a bearing of 060° to Y. He then travels a distance of 18km to a point Z and Z is 30km from X.
(i) Draw the diagram to show the positions of X, Y and Z ; (ii) What is the bearing of Z from Y ; (iii) Calculate the bearing of X from Z.
Explanation
(a) 
From the diagram and by Pythagoras theorem,
\(|PR|^{2} = |PQ|^{2} + |QR|^{2}\)
\(|PR|^{2} = (3a)^{2} + (4a)^{2}\)
\(|PR|^{2} = 9a^{2} + 16a^{2} = 25a^{2}\)
\(|PR| = \sqrt{25a^{2}} = 5a\)
(b) 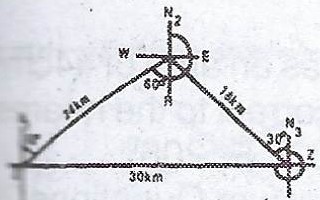
(ii) From the figure, Bearing of Y from X = 060°
Using cosine rule,
\(\cos XYZ = \frac{24^{2} + 18^{2} - 30^{2}}{2 \times 24 \times 18}\)
\(\cos XYZ = 0 \implies < XYZ = 90°\)
\(< RYZ = 90° - 60° = 30°\)
\(< N_{2} YZ = 180° - 30° = 150°\) (angles on a straight line)
The bearing of Z from Y is 150°.
(iii) \(\cos XZY = \frac{30^{2} + 18^{2} - 24^{2}}{2 \times 30 \times 18}\)
= \(\frac{900 + 324 - 576}{1080}\)
\(\cos XZY = \frac{648}{1080} = 0.6\)
\(< XZY = \cos^{-1} (0.6) = 53.13°\)
\(\therefore\) The bearing of X from Y = 360° - (53.13° + 30°) = 276.87°.

