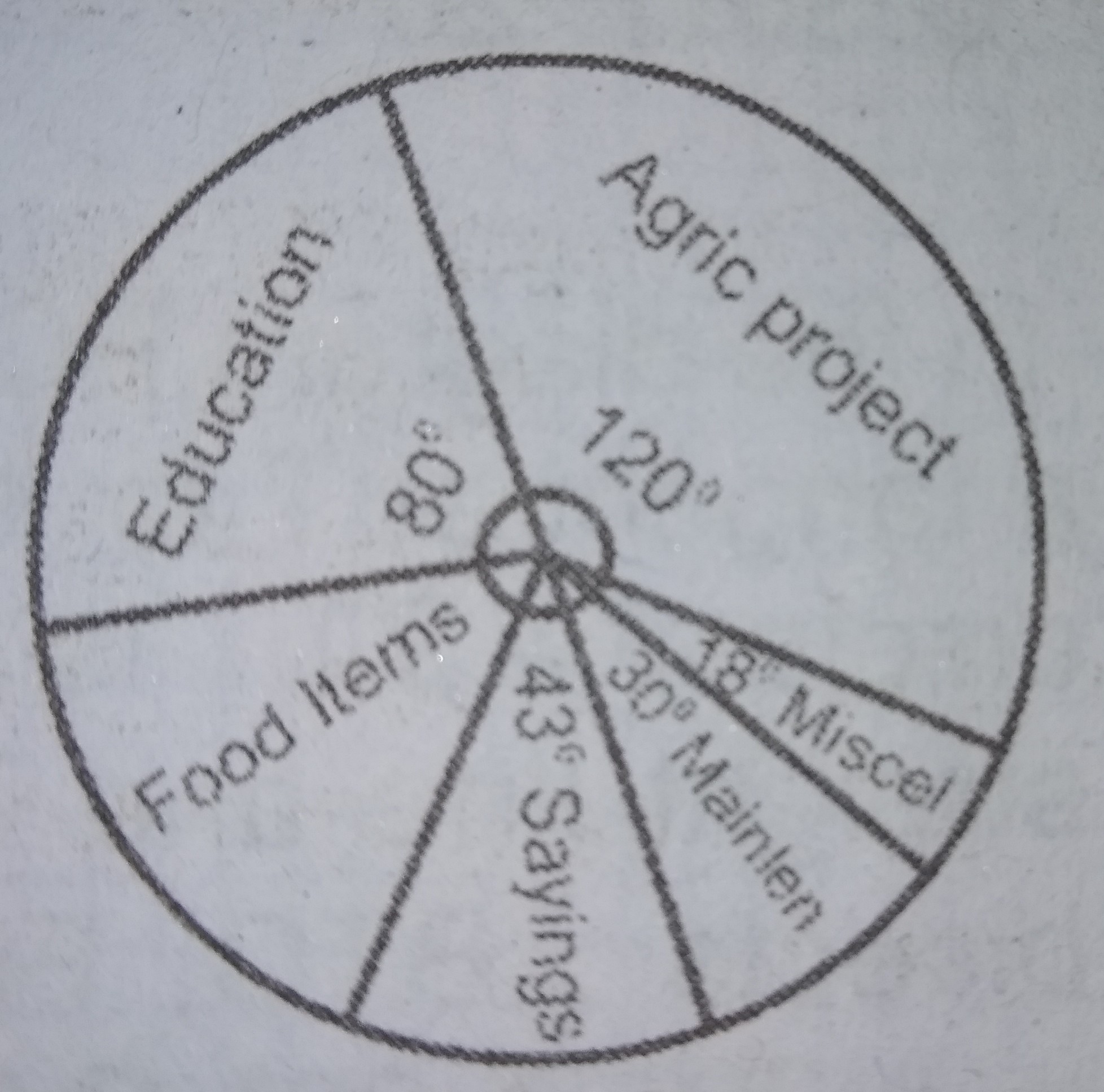
The annual salary of Mr. Johnson Mohammed for 1989 was N12,000.00. He spent this on agriculture projects, education of his children, food items, saving , maintenance and miscellaneous items as shown in the pie chart
How much did he spend on food items?
- A. N9,700.00
- B. N6,700.00
- C. N2,000.00
- D. N4,000.00
- E. N2,300.00
An aeroplane flies from a town P(lat. 40°N, 38°E) to another town Q(lat. 40°N, 22°W). It later flies to a third town T(28°N, 22°W). Calculate the :
(a) distance between P and Q along their parallel of latitude ;
(b) distance between Q and T along their line of longitudes;
(c) average speed at which the aeroplane will fly from P to T via Q, if the journey takes 12 hours, correct to 3 significant figures. [Take the radius of the earth = 6400km ; \(\pi = 3.142\)]
In a class of 40 students, 25 speak Hausa, 16 speak Igbo, 21 speak Yoruba and each of the students speak at least one of the these three languages. If 8 speak Hausa and Igbo, 11 speak Hausa and Yoruba and 6 speak Igbo and Yoruba.
(a) Draw a Venn diagram to illustrate the information, using x to represent the number of students that speak all three languages.
(b) calculate the value of x.
The following is an incomplete table for the relation \(y = 2x^{2} – 5x + 1\)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 8 | 1 | -1 | 26 |
(a) Copy and complete the table.
(b) Using a scale of 2cm to 1 unit on the x- axis and 2cm to 10 units on the y- axis, draw the graph of the relation \(y = 2x^{2} – 5x + 1\) for \(-3 \leq x \leq 5\).
(c) Using the same scale and axes, draw the graph of \(y = x + 6\).
(d) Estimate from your graphs, correct to one decimal place : (i) the least value of y and the value of x for which it occurs ; (ii) the solution of the equation \(2x^{2} – 5x + 1 = x + 6\).
(a) If a number is chosen at random from the integers 5 to 25 inclusive, find the probability that the number is a multiple of 5 or 3.
(b) A bag contains 10 balls that differ only in colour; 4 are blue and 6 are red. Two balls are picked one after the other, with replacement. What is the probability that:
(i) both are red? (ii) both are the same colour?
(a) ABCD is a trapezium in which AB // DC, |AB| = 8cm, < ABC = 60°, |BC| = 5.5cm and |BD| = 8.3cm. Using a ruler and a pair of compasses only, construct:
(i) the trapezium ABCD ; (ii) a rectangle PQCD, where P, Q are two points AB;
(b) Measure |AB| and |QB|.
The weights to the nearest kilogram, of a group of 50 students in a College of Technology are given below:
65, 70, 60, 46, 51, 55, 59, 63, 68, 53, 47, 53, 72, 53, 67, 62, 64, 70, 57, 56, 73, 56, 48, 51, 58, 63, 65, 62, 49, 64, 53, 59, 63, 50, 48, 72, 67, 56, 61, 64, 66, 52, 49, 62, 71, 58, 53, 69, 63, 59.
(a) Prepare a grouped fraquency table with class intervals 45 – 49, 50 – 54, 55 – 59 etc.
(b) Using an assumed mean of 62 or otherwise, calculate the mean and standard deviation of the grouped data, correct to one decimal place.
(a) Find the volume of a right solid cone of base radius 4cm and perpendicular height 6cm. [\(\pi = 3.142\)]
(b) A hemispherical tank of diameter which is 10m is filled by water issuing from a pipe of radius 20cm at 2m per second. Calculate, correct to three significant figures, the time, in minutes, it takes to fill the tank.
The feet of two vertical poles of height 3m and 7m are in line with a point P on the ground, the smaller pole being between the taller pole and P and at a distance of 20m from P. The angle of elevation of the top (T) of the taller pole from the top (R) of the smaller pole is 30°. Calculate the :
(i) distance RT ; (ii) distance of the foot of the taller pole from P, correct to three significant figures ; (iii) angle of elevation of T from P, correct to one decimal place.
A carpenter was told to make a rectangular desk with top of dimension 50cm by 40cm. The carpenter actually made the desk 60cm by 35cm.
(a) Calculate the percentage error in the (i) length and the breadth ; (ii) area of the table top.
(b) Find the product of the two errors in a(i).
(a) Prove that the sum of the angles in a triangle is 2 right angles.
(b) The side AB of a triangle ABC is produced to a point D. The bisector of ACB cuts AB at E. Prove that < CAE + < CBD = 2 < CEB.
Show on a graph, the area which gives the solution set of the inequalities: \(y – 2x \leq 4 ; 3y + x \geq 6 ; y \geq 7x – 9\).
(a) Simplify \(\frac{0.016 \times 0.084}{0.48}\) [Leave your answer in standard form].
(b) Eight wooden poles are to be used for pillars and the lengths of the poles form an Arithmetic Progression (A.P). If the second pole is 2m and the sixth is 5m, give the lengths of the poles, in order.
Two groups of male students cast their vote on a particular proposal. The results are as follows:
| In favor | Against | |
| Group A | 128 | 32 |
| Group B | 96 | 48 |
If a student is chosen at random, what is probability that he is against the proposal?
- A. 3/19
- B. 4/19
- C. 5/19
- D. 9/19
- E. 10/19
Two groups of male students cast their votes on a particular proposal. The result are as follows:
| In favor | Against | |
| Group A | 128 | 32 |
| Group B | 96 | 48 |
If a student in favor of the proposal is selected for a post, what is the probability that he is from group A?
- A. 8/19
- B. 16/35
- C. 10/19
- D. 4/7
- E. 4/5
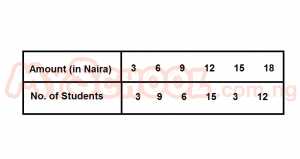
The table shows that the amount of money (in naira)collected through voluntary donations in a secondary school.
What is the median of distribution
- A. N3.00
- B. N9.00
- C. N12.00
- D. N15.00
- E. N18.00
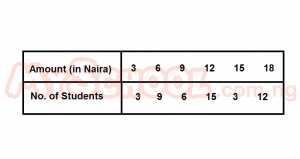
The table shows that the amount of money (in naira)collected through voluntary donations in a secondary school. What is the mode?
- A. N3
- B. N6
- C. N9
- D. N12
- E. N15
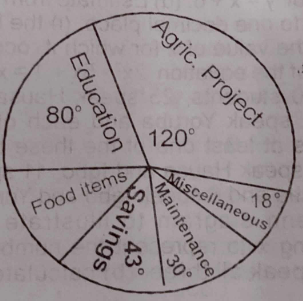
The annual salary of Mr. Johnson Mohammed for 1989 was N12,000.00. He spent this on agriculture projects, education of his children, food items, saving , maintenance and miscellaneous items as shown in the pie chart
How much money did he invest in agriculture?
- A. N1,200.00
- B. N1,440.00
- C. N2,000.00
- D. N2,910.00
- E. N4,000.00
The bearing of a point X from a point Y is 074°. What is the bearing of Y from X?
- A. 106o
- B. 146o
- C. 164o
- D. 254o
- E. 286o
From the top of a building 10m high, the angle of depression of a stone lying on the horizontal ground is 69o. Calculate ,correct to one decimal place, the distance of the stone from the foot of the building
- A. 3.6m
- B. 3.8m
- C. 6.0m
- D. 9.3m
- E. 26.1m
If the shadow of a pole 7m high is 1/2 its length what is the angle of elevation of the sun, correct to the nearest degree?
- A. 90o
- B. 63o
- C. 60o
- D. 26o
- E. 0o


