The feet of two vertical poles of height 3m and 7m are in line with a point P on the ground, the smaller pole being between the taller pole and P and at a distance of 20m from P. The angle of elevation of the top (T) of the taller pole from the top (R) of the smaller pole is 30°. Calculate the :
(i) distance RT ; (ii) distance of the foot of the taller pole from P, correct to three significant figures ; (iii) angle of elevation of T from P, correct to one decimal place.
Explanation
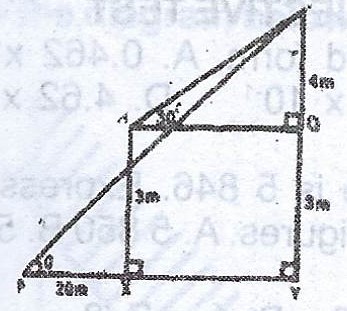
(i) From the figure,
\(\sin 30° = \frac{4}{RT} \implies RT = \frac{4}{\sin 30°}\)
= \(\frac{4}{0.5} = 8m\)
(ii) |RQ| = |XY|
\(\therefore |XY|^{2} = 8^{2} - 4^{2} = 64 - 16 = 48\)
\(|XY| = \sqrt{48} = 4\sqrt{3} m = 6.928m\)
But |PY| = |PX| + |XY|
= 20 + 6.928 = 26.928m \(\approxeq\) 26.9m.
(iii) Let the angle of elevation = \(\theta\)
\(\tan \theta = \frac{TY}{PY} = \frac{7}{26.928}\)
\(\tan \theta = 0.26 \implies \theta = \tan^{-1} (0.26)\)
\(\theta = 14.57° \approxeq 14.6°\) (to 1 decimal place)

