(a) Find the volume of a right solid cone of base radius 4cm and perpendicular height 6cm. [\(\pi = 3.142\)]
(b) A hemispherical tank of diameter which is 10m is filled by water issuing from a pipe of radius 20cm at 2m per second. Calculate, correct to three significant figures, the time, in minutes, it takes to fill the tank.
Explanation
(a) 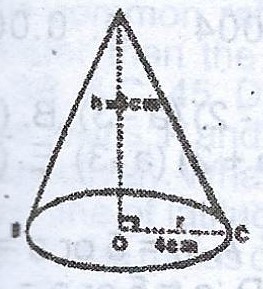
Formula : Volume = \(\frac{1}{3} \pi r^{2} h\)
\(\pi = 3.142; r = 4cm; h = 6cm\)
\(Volume = \frac{1}{3} \times 3.142 \times 4^{2} \times 6 = 100.544 cm^{3}\)
(b) 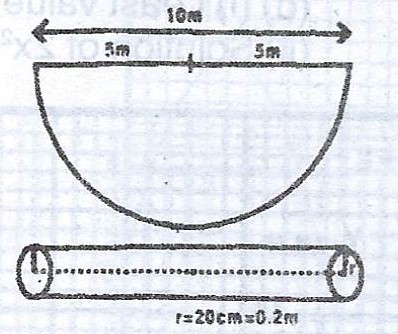
Volume of hemisphere = \(\frac{1}{2} \times \frac{4}{3} \pi r^{3}\)
= \(\frac{2}{3} \times \frac{22}{7} \times 5^{3}\)
= \(\frac{5500}{21} cm^{3} = 261.905 cm^{3}\)
Volume of water discharged per second = \(\pi r^{2} h\)
= \(\frac{22}{7} \times 0.2m \times 0.2m \times 2m = \frac{1.76}{7}\)
= \(0.2514 m^{3} / sec\)
\(\therefore \text{The time to fill the tank = } \frac{261.905}{0.2514 \times 60}\)
= \(\frac{261.905}{15.084} = 17.363 mins\)
\(\approxeq 17.4 mins\)

