The following is an incomplete table for the relation \(y = 2x^{2} – 5x + 1\)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 8 | 1 | -1 | 26 |
(a) Copy and complete the table.
(b) Using a scale of 2cm to 1 unit on the x- axis and 2cm to 10 units on the y- axis, draw the graph of the relation \(y = 2x^{2} – 5x + 1\) for \(-3 \leq x \leq 5\).
(c) Using the same scale and axes, draw the graph of \(y = x + 6\).
(d) Estimate from your graphs, correct to one decimal place : (i) the least value of y and the value of x for which it occurs ; (ii) the solution of the equation \(2x^{2} – 5x + 1 = x + 6\).
Explanation
(a) \(y = 2x^{2} - 5x + 1\)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 34 | 19 | 8 | 1 | -2 | -1 | 4 | 13 | 26 |
Table of value for \(y = x + 6\)
| x | -2 | 0 | 2 |
| y | 4 | 6 | 8 |
(b) 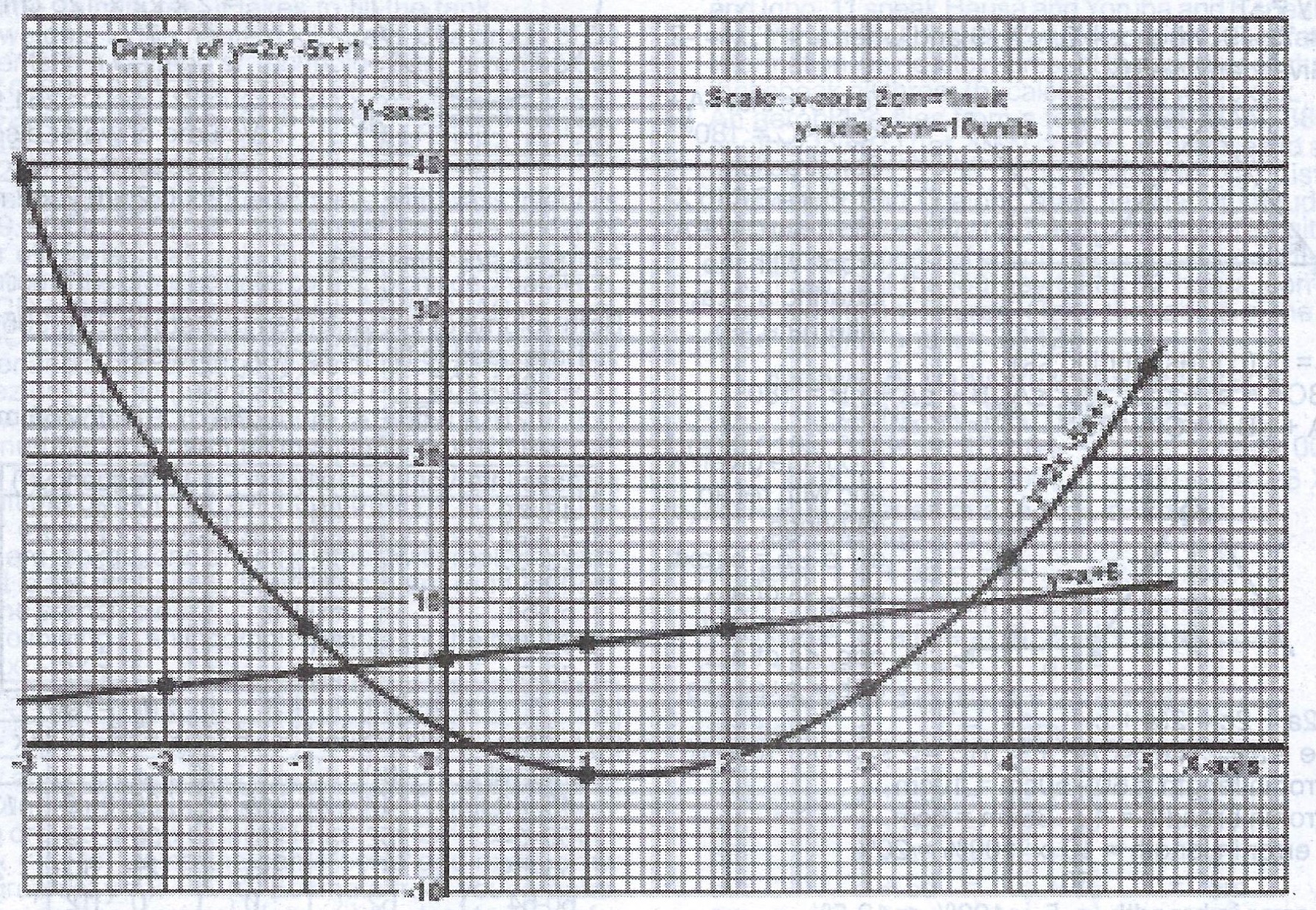
(d) (i) Least value of y = -2 occurs at x = 1
(ii) Solution of \(2x^{2} - 5x + 1 = x + 6\) are x = -0.7 and x = 3.7.

