From a horizontal distance of 8.5 km, a pilot observes that the angles of depression of the top and the base of a control tower are 30° and 33° respectively. Calculate, correct to three significant figures :
(a) the shortest distance between the pilot and the base of the control tower;
(b) the height of the control tower.
(a) Using a ruler and a pair of compasses only, construct a parallelogram PQRS with diagonals |PR| = 9cm and |QS| = 6cm, intersecting at K and < QKR = 60°.
(b) Construct a rectangle PABS which is equal in area to PQRS in (a) above and on the same side of PS as PQRS. Measure |PA|.
The table below shows the distribution of the waiting times for some customers in a certain petrol station.
| Waiting time (in mins) | No of customers |
| 1.5 – 1.9 | 3 |
| 2.0 – 2.4 | 10 |
| 2.5 – 2.9 | 18 |
| 3.0 – 3.4 | 10 |
| 3.5 – 3.9 | 7 |
| 4.0 – 4.4 | 2 |
(a) Write down the class boundaries of the distribution.
(b) Construct a cumulative frequency curve for the data;
(c) Using your graph, estimate: (i) the interquartile range of the distribution ; (ii) the proportion of customers who could have waited for more than 3 minutes.
(a) Prove that the angle which an arc of a circle subtends at the centre is twice that which it subtends at any point on the remaining part of the circumference.
(b) 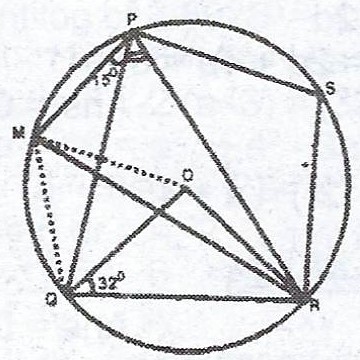
In the diagram, O is the centre of the circle, < OQR = 32° and < MPQ = 15°. Calculate (i) < QPR ; (ii) < MQO.
Using a scale of 2cm to 1 unit on the x- axis and 1cm to 1 unit on the y- axis, draw on the same axes the graphs of \(y = 3 + 2x – x^{2}; y = 2x – 3\) for \(-3 \leq x \leq 4\). Using your graph:
(i) solve the equation \(6 – x^{2} = 0\);
(ii) find the maximum value of \(3 + 2x – x^{2}\);
(iii) find the range of x for which \(3 + 2x – x^{2} \leq 1\), expressing all your answers correct to one decimal place.
A man bought 5 reams of duplicating paper, each of which are supposed to contain 480 sheets. The actual number of sheets in the packets were : 435, 420, 405, 415 and 440.
(a) Calculate, correct to the nearest whole number, the percentage error for the packets of paper;
(b) If the agreed price for a full ream was N35.00, find, correct to the nearest naira, the amount by which the buyer was cheated.
(a) Solve the equation, correct to two decimal places \(2x^{2} + 7x – 11 = 0\)
(b) Using the substitution \(P = \frac{1}{x}; Q = \frac{1}{y}\), solve the simultaneous equations : \(\frac{2}{x} + \frac{1}{y} = 3 ; \frac{1}{x} – \frac{5}{y} = 7\)
ABCDE is a regular pentagon and a rectangle AXYE is drawn on the side AE such that the vertices X and Y lie on the sides BC and CD respectively. Calculate the size of
(i) an interior angle of the pentagon ;
(ii) < BXA.
A man has 9 identical balls in a bag. Out of these, 3 are black, 2 are blue and the remaining are red.
(a) If a ball is drawn at random, what is the probability that it is (i) not blue? (ii) not red?
(b) If 2 balls are drawn at random, one after the other, what is the probability that both of them will be (i) black, if there is no replacement? (ii) blue, if there is a replacement?
In a certain class, 22 pupils take one or more of Chemistry, Economics and Government. 12 take Economics (E), 8 take Government (G) and 7 take Chemistry (C). Nobody takes Economics and Chemistry and 4 pupils take Economics and Government.
(a)(i) Using set notation and the letters indicated above, write down the two statements in the last sentence; (ii) Draw a Venn diagram to illustrate the information.
(b) How many pupils take (i) both Chemistry and Government ? (ii) Government only?
(a) Using logarithm table, evaluate \(\frac{\sqrt[3]{1.376}}{\sqrt[4]{0.007}}\) correct to three significant figure.
(b) Without using Mathematical tables, find the value of \(\frac{\log 81}{\log \frac{1}{3}}\).
Simplify :
(i) \(2\frac{2}{3} – (2\frac{1}{2} – 1\frac{4}{5})\)
(ii) \(\frac{3.25 – 1.64}{2.47 – 2.01}\)
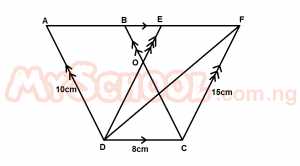
In the diagram above , |AD| = 10cm, |DC| = 8cm and |CF| = 15cm. Which of the following is correct?
- A. Area BCF = Area DCF
- B. Area ADE = Area ADF
- C. Area ADE = Area DCFE
- D. Area CBF = Area DABC
- E. Area DABO = Area CFEO
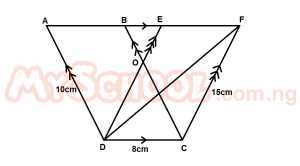
In the diagram above , |AD| = 10cm, |DC| = 8cm and |CF| = 15cmIf the area of triangle DCF = 24cm2, find the area of the quadrilateral ABCD.
- A. 24cm2
- B. 48cm2
- C. 80cm2
- D. 96cm2
- E. 120cm2
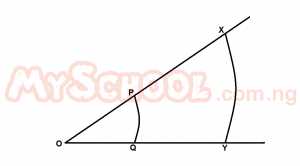
In the diagram above, PQ and XY are two concentric arc; center O, the ratio of the length of the two arc is 1:3, find the ratio of the areas of the two sectors OPQ and OXY
- A. 1:3
- B. 1:6
- C. 1:9
- D. 2:3
- E. 4:9
Find the area of an equivalent triangle of side 16cm
- A. 64√3cm2
- B. 72√3cm2
- C. 96cm2
- D. 128√3cm2
- E. 128cm2
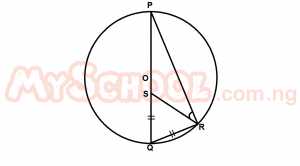
In the diagram above, O is the center of the circle, |SQ| = |QR| and ∠PQR = 68°. Calculate ∠PRS
- A. 34o
- B. 45o
- C. 56o
- D. 62o
- E. 68o
In a given regular polygon, the ratio of the exterior angle to the interior angles is 1:3. How many side has the polygon?
- A. 40
- B. 5
- C. 6
- D. 8
- E. 12
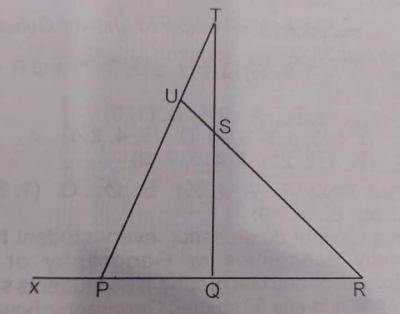
In the diagram above, ∠PTQ = ∠URP = 25° and XPU = 4URP. Calculate ∠USQ.
- A. 100o
- B. 120o
- C. 125o
- D. 130o
- E. 150o
The angles of a pentagon are x°, 2x°, (x + 60)°, (x + 10)°, (x -10)°. Find the value of x.
- A. 40
- B. 60
- C. 75
- D. 80
- E. 90
Which of the following about a rhombus may not be true?
- A. The diagonals are equal
- B. The diagonals bisect the angles through which they pass
- C. the diagonals bisect each other
- D. The adjacent sides are equal
- E. Opposite angles are equal


