In a certain class, 22 pupils take one or more of Chemistry, Economics and Government. 12 take Economics (E), 8 take Government (G) and 7 take Chemistry (C). Nobody takes Economics and Chemistry and 4 pupils take Economics and Government.
(a)(i) Using set notation and the letters indicated above, write down the two statements in the last sentence; (ii) Draw a Venn diagram to illustrate the information.
(b) How many pupils take (i) both Chemistry and Government ? (ii) Government only?
Explanation
(a) 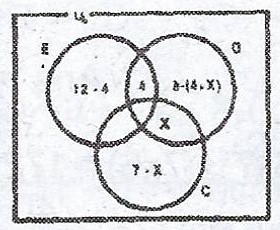
(i) Nobody takes Economics and Chemistry \(n(E \cap C) = \null \).
(ii) 4 pupils take Economics and Government; \(n(E \cap G) = 4\)
(b) (i) Suppose \(n(C \cap G) = x\)
\(22 = 8 + 4 + 8 - 4 - x + x + 7 - x\)
\(22 = 23 - x \implies x = 1\)
Only 1 person does Chemistry and Government.
(ii) Number taking only Government = \(8 - (4 + x)\)
\(8 - (4 + 1) = 3\)

